Valós idejű Sugárkövetés
Erdős Zoltán
Budapest
2020.
Tartalomjegyzék
2. Klasszikus DirectX9 és OpenGL2:
3. Újítás: Valós idejű DirectX RayTracing és RadeonRays:
4. Saját Sugárkövetés program:
4.2.1 Sugarak-háromszögek ütközésvizsgálata, párhuzamosan:
4.2.2 Ütközésdetektálás gyorsítás, tér felosztással (BVH):
4.2.3 BVH gyors újra építése, ha a csúcsok megváltoztak:
5. Textúrázás Barycentrikus koordinátákkal:
6.4 GenerateCameraRays Shader:
7. Fények és árnyék számítása RayShader-ben:
8. A ’class Scene’ osztály feladata:
8.1 Statikus objektum betöltése, ’class OBJLoader’ osztály segítségével:
8.2 Dinamikus objektum betöltése, „class SMDLoader” osztály segítségével:
9. Osztály-, Objektum-, és Használati eset diagram:
10. Továbbfejlesztési lehetőségek:
1. Bevezetés:
Azért a sugárkövetés témát választottam szakdolgozatnak, mert érdekelt, hogy meg tudom-e csinálni ezt a feladatot. C# nyelven nem találtam forráskódot ebből a témából. Illetve most aktuális ez a téma, pl. a következő Playstation5 támogatni fogja a sugárkövetést hardveresen. Érdekel ez a téma.
Régóta létezik 3D-s megjelenítés. A számítógépek teljesítménye nem képes valós időben fénykép minőségű kép előállítására, ezért közelítő megoldásokat találtak ki. A közelítő megoldások sokkal gyorsabbak, elfutnak kisebb teljesítményű számítógépeken, viszont nem élethű képet adnak eredményűl.
Az 1995-ös években az akkori játékok a háromszög csúcsainak adataiból számolták ki egy pixel színét a barycentrikus koordináták segítségével (VertexShader), ez gyors. Majd a 2002-es években lehetett a pixelek színét (PixelShader) egyedileg programozni, ez lassabb, de jelenleg ez is elég gyors már [19]. Itt is még csak korlátozott adatok álltak rendelkezésre egy pixel színének kiszámításához. Nem volt információ (egy pixel színének számításakor) arról, hogy a legközelebbi háromszög, ami a képernyőn megjelenik, az mögött mi van.
Mostanság a 2016-os években annyira megnőtt a
számítógépek teljesítménye, hogy lehet alkalmazni a „sugárkövetést” [18]. Így
nem csak a legközelebb álló háromszög adatait ismerjük, hanem a mögötte lévőket
is el tudjuk érni. A „sugárkövetés”, amit be szeretnék mutatni, ez a megoldás a
mai számítógépeken elfogadható sebességgel fut, élethűbb képet lehet elő
állítani vele. Van tükröződés és törés, amivel, ha egy pixel színét számolom,
akkor a szomszédos testekről visszaverődő fény színét is számításba tudom venni
[18]. De még ez a megoldás sem fénykép minőségű, hiszen sugárkövetésnél
pontosan egy sugarat indítok tükröződés és törés irányba. Míg a valóságban van
egy kis fény szóródás, mivel a felületek, amin pattan vagy törik a fény, nem
tükörsima.
A „Globális illumináció” az a megoldás, ami túlmutat a jelenlegi sugárkövetésen,
és még élethűbb képet állít elő, de az gépigényesebb mint a sugárkövetés [18].
2. Klasszikus DirectX9 és OpenGL2:
Ide vehető a 2002-ben megjelent VertexShader és PixelShader. Nem látni a háromszögek mögé, csak a legközelebbi háromszöget látjuk [19].
3. Újítás: Valós idejű DirectX RayTracing és RadeonRays:
2016-ban, jelentek meg az első valós idejű sugárkövetés megoldások. AMD oldalon, ami platformfüggetlen, a „RadeonRays SDK” jelent meg, ami CPU, OpenCL vagy Vulkan segítségével számol. A Microsoft a „DirectX12 RayTracing SDK”, ami naprakész, viszont (úgy tudom) csak Windows 10-en fut. Az Intelnek és az NVidia-nak is vannak sugárkövetés SDK-juk.
4. Saját Sugárkövetés program:
Ha vannak nagy cégektől sugárkövetés SDK-k, akkor miért írok sajátot (ami butább)?
Kíváncsiságból. Azért is írom, hogy megértsem ennek a működését.
A forráskód amit írtam/írok, letölthető a https://github.com/ezszoftver/OpenCLRenderer weboldalról. OpenCL-t használok a párhuzamos számításokhoz. Szabadon felhasználható, módosítható a forráskód, nincs licensz védelem alatt.
4.1 Elmélet röviden:
A sugárkövetés „futószalagja” elméletben így működik:
1. sugarakat indítok a kamerából, amik elmetszhetnek háromszögeket.
2. ha egy sugár-háromszög metszés van, akkor abból az ütközéspontból kiszámolom, hogy mennyi fény éri azt a pontot, majd újabb sugarakat indíthatok tükröződési és törési irányba. Ez a sugár újra elmetszhet egy háromszöget, és kezdődik ez a lépés újra [18].
3. Kb. 3 ütközés után abba hagyom az ütközés keresést, meg vannak a szín információk, amiből a képernyőn megjelenő pixel színét ki tudom számolni. Azért hagyom abba a további ütközéskeresést, mert, ha valós idejű képet szeretnék előállítani, akkor tovább folytatni gépigényes. Így is jobban megközelítem a valóságot, mint a 2002-es DirectX9/OpenGL2 -vel.
Elméletben ennyi. Vajon mik azok a megoldások, amivel rövid idő alatt el lehet a „futószalagot” végezni? Most ezt mutatom be.
Fontos! Amit leírok megoldásokat, nem a leggyorsabb megoldások, én ezeket ismerem, ezeket tudom bemutatni.
4.2 Gyorsítási lehetőségek:
4.2.1 Sugarak-háromszögek ütközésvizsgálata, párhuzamosan:
Először be szeretném mutatni, hogyan lehet egy „sugár-háromszög” metszéspont vizsgálatot elvégezni [18]. Majd bemutatom, hogyan lehet, ha sok sugarunk van, ezt gyorsítani (elöljáróban annyi, hogy ahány sugarunk van, annyi szálat kell indítani OpenCL segítségével, és úgy elvégezni a „sugár-háromszögek” metszéspont vizsgálatot). Az „OpenCL” script kód nem a CPU-n, hanem a videokártyán fut.
A „sugár-háromszög” metszéspont vizsgálat lépései:
- „pont-sík” távolsága
- „sugár-sík” távolsága
- metszéspont kiszámítása
- metszéspont a háromszögen belül van? vizsgálat
pont-sík távolsága:
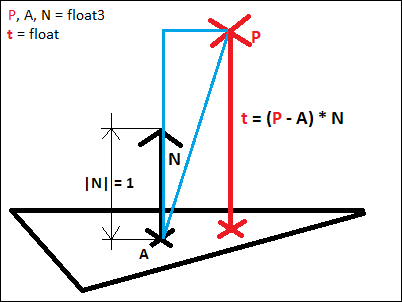
1. ábra: pont-sík távolsága [saját]
Előszöt „float t” -t kell kiszámolni. Tekintsük úgy most a háromszöget, mintha az egy sík lenne. Egy síkot meghatároz egy „float3 A” pont, amit a sík elmetsz, és egy „float3 N” irány, hogy merre néz a sík.
Ha a „float3 (P - A)” vektort skalárisan össze szorozzuk az 1.0 egységnyi hosszú „float3 N” vektorral, akkor megkapjuk „float t” -t [18].
Két „float3 a,b” egységnyi hosszú vektorok skaláris szorzatára, igaz ez a képlet:
a * b = cos(alpha)
„(P - A)” és „N” vektorok skaláris szorzatának képlete:
(P - A) * N = cos(alpha) * |P - A|
cos(alpha) eredménye, [-1.0 .. +1.0] intervallum béli számot ad eredményűl.
Tehát |P - A| hosszt összeszorozzuk egy +1.0 -nál kisebb számmal, így eredményül egy
|P - A| -nál rövidebb, „t” hosszt ad eredményül, ami a sík és a „P” pont távolsága.
sugár-sík távolsága:
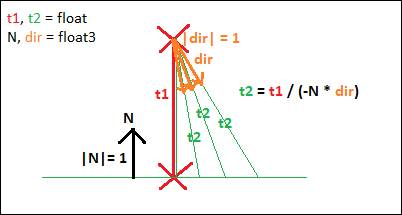
2. ábra: sugár-sík távolsága [saját]
Ha meg van a t távolság, akkor, ha figyelembe vesszük azt, hogy a „P” pontnak van iránya is, akkor egy félegyenest kapunk. Ha az irány megegyezik a -N -el, akkor az a legrövidebb távolság. Ahogyan a „t2” -k mutatják a 2. ábrán úgy, ha minél nagyobb a „-N, dir” közötti szög, annál hosszabb „t2” -ket kapunk eredményül [18].
metszéspont kiszámítása:
Azt a pontot, hogy a félegyenes hol metszi el a síkot ezzel a képlettel kapjuk meg:
P2 = P + (dir * t2);
„float3 P2” az a pont, amit a sík elmetsz [18]. A „float3 P” és „float3 dir” a félegyenes (sugár) kezdőpontja és iránya.
A „float3 dir” hossza, 1 egység.
metszéspont a háromszögen belül van?:
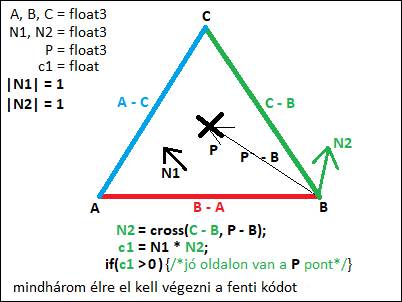
3. ábra: a metszéspont a háromszögen belül van? [saját]
A harmadik lépés, hogy a síkot metsző pont a háromszögen belül van-e? Én azt a megoldást választottam, hogy vektoriális szorzattal ellenőrzöm ezt [18]. A háromszög mindhárom élére el kell végezni, a „jó oldalon van a pont?” ellenőrzést. Én egy élre mutatom be az ellenőrzést:
Vegyünk B-C szakaszt. Ha vektoriálisan össze szorzom (C - B) és (P - B) vektorokat, akkor a képen látható N2 vektort kapom eredményűl. Fontos, hogy a vektoriális szorzat nem kommutatív, vagyis, ha nem ebben a sorrendben, hanem fordítva végzem el a vektoriális szorzatot (cross(P - B, C - B)), akkor -N2 -t kapok. Majd szög ellenőrzéssel (skaláris szorzat) ellenőrzöm, hogy jó oldalon van-e a P pont. Összeszorzom skalárisan a háromszög normal vektorját(N1), az N2-vel. Ha a két normalvektor közötti szög kissebb mint 90fok, akkor a „P” pont, a „C - B” él jó oldalán áll. Mind a három élre igaznak kell lennie, hogy a szög kisebb-e mint 90fok. h Ekkor a „háromszögen belül vagyok-e?” kérdésre a válasz, igaz. A vektoriális szorzatnál figyelembe kell venni azt is, hogy nem mindegy, hogy (C - B) vagy (B - C), mert, ha felcserélem a pontokat, akkor ellenkező irányba fog mutatni a vektor. Én az óramutató járásával ellentétes irányt választottam.
Tehát el tudok mostantól végezni a félegyenes-háromszög ütközésvizsgálatot. Félegyenes alatt sugarat, vagy ray -t is mondhatok, mindhárom szó most ugyanazt jelenti. Amikor egy képet akarok előállítani sugárkövetéssel, akkor minden egyes pixelből sugarat indítok a világba. Tehát nagyon sok sugarat kell indítanom. Két pixelnek a textúrából, nincs köze egymáshoz, tehát két sugárnak sincs köze egymáshoz. Nincs függőség, vagyis pl. a (0,0) pixelből indított sugár, nem várakozik a (0,1) pixelből indított sugárra, tehát párhuzamosan, külön-külön szálakon lehet elindítani a sugár-háromszög metszésvizsgálatot.
Egy videokártyában kb. 100-2000 darab kis órajelű (500Mhz – 1GHz) processzor van. Ezeket a processzorokat el lehet érni C nyelven, „OpenCL” segítségével. Tehát tudok párhuzamosítani „hardveresen”. A CPU abban más a GPU-k tól, hogy magasabb órajelen működnek, kevesebb van belőlük (1 – 16 mag), viszont összetettebb, az egész számítógépet vezérlik. CPU-n lassabban fut egy kép számítás, mint egy videokártyán. Pont azért találták ki a videokártyát, vagyis egy külön hardvert képszámításra, mert az a képszámításra van optimalizálva, gyorsabban kiszámolja a képet.
OpenCL-ben, „Buffer” -ekben vannak tárolva az adatok. Egy „Buffer” osztály, más néven tömb. Meg lehet adni a „Buffer” -nek, hogy milyen típusú adatokat akarok benne tárolni: Buffer<int> egesz_szamok;. Ez a buffer a videokártya memóriájában jön létre. Általában van egy bemeneti Buffer, amivel számol, és van egy kimeneti Buffer, ahova az eredmények kerülnek. Majd a Buffer-t ha kell, vissza lehet másolni az operációs rendszer memóriába, és lehet az eredményekkel tovább számolni.
Tehát van sok sugaram, ez egy „Buffer” (Buffer<Ray> rays). Illetve van a háromszögeket tartalmazó „Buffer” (Buffer<Triangle> triangles). Ezek a bemenő bufferek. Kell egy kimeneti buffer is, ami megmondja, hogy egy sugár elmetszette-e a „triangles” bufferben lévő háromszögek valamelyikét. Ezek az adatok az eredmény (Buffer<hit> hits). „hits” Buffer annyi elemet tartalmaz, ahány sugarunk van.
Két párhuzamosan, külön-külön szálon futó Ray, ugyanazt a „triangles” buffert használja, baj ez? Nem, mert csak olvasnak belőle, nem módosítják.
Egy videokártya, kb. 10x gyorsabban kiszámol egy képet a párhuzamosítás miatt, mint egy vele egyenértékű CPU.
A sugarakat párhuzamosítottuk. Most nézzük meg, hogy mit lehet tenni a háromszögekkel, ott is gyorsítani kéne.
4.2.2 Ütközésdetektálás gyorsítás, tér felosztással (BVH):
Eddig egy sugár végig járta, az összes háromszöget, és úgy kereste a hozzá legközelebbi, elmetsző háromszöget. Nem lehet ezen gyorsítani? De lehet, tér felosztással [18][21].
Képzeljük el, hogy van a világ. Az legyen mondjuk 1km hosszú, 1km magas, 1km széles). Itt vannak a háromszögek elszórva. Van egy sugarunk, pl. (10,10,10) pontban. Felesleges azokkal a háromszögekkel ütközéstdetektálást végezni, amik nagyon messze, pl. (1km, 1km, 1km) távolságra vannak a Ray-től. Jobb lenne, csak a Ray-hoz közeli háromszögeket vizsgálni. Megoldás, daraboljuk fel a teret, minden altérbe másoljuk bele, a teret elmetsző háromszögeket. Majd, ha jön egy sugár, akkor számoljuk ki hogy a sugár megy tér részeket metsz el, és csak az azokban a tér részekben lévő háromszögekkel végezzünk ütközés keresést.
Én itt, a BVH (Bounding Volume Hierarchy) megoldást választottam [21]. Jelentése: alterek, szülő-gyerek kapcsolatban, vagyis hierarchiában.
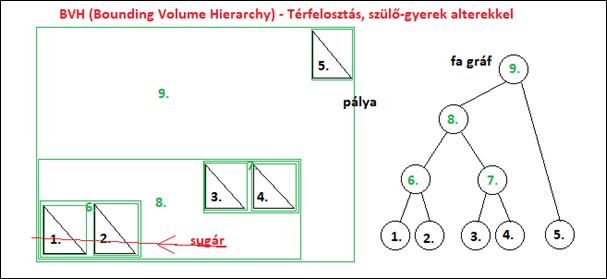
4. ábra: BVH (alterek a gyors kereséshez) [saját]
A kép bal oldali része az altereket, világot mutatja jól, míg a kép jobb oldali része, a gráfot, a szülő gyerek kapcsolatokat mutatja jól.
Az 1,2,3,4,5 csomópontok, háromszögek, míg a 6,7,8,9 csomópontok, tér részek (bounding box). A 9. csomópont, a gráf szerint, az a gyökér, az az egész világot magába foglalja.
Vizsgáljunk a sugár szemszögéből, ami a 4. ábrán van: amit elmetsz az a 9, 8, 6 -os alterek, és az 1, 2 -es háromszögek. Felesleges vizsgálni a 3, 4, 5-ös háromszögekkel a metszésvizsgálatot.
Hogyan kapjuk meg az 1 és 2-es háromszögeket? Kezdjük a metsző háromszögek keresést a fa gráf bejárásával.
- A sugár elmetszi a gyökeret? (9) => igen, tehát vizsgáljuk meg a 9. csomópont gyerekeit.
- A sugár elmetszi a 5 alteret? nem, tehát erre nem folytatjuk a keresést.
- A sugár elmetszi a 8-as alteret? igen, vizsgáljuk meg ennek az altérnek/csomópontnak a gyerekeit.
- a sugár elmetszi a 7-es alteret? nem, erre nem keresünk tovább.
- a sugár elmetszi a 6-os alteret? igen, akkor vizsgáljuk ennek az altérnek/csomópontnak a gyerekeit.
- a sugár elmetszi az 1 háromszöget? igen
- a sugár elmetszi a 2-es háromszöget? igen
Levél: Az a csomópont, akinek nincsen gyereke (a fa gráf alja), vagyis egy háromszög van benne.
Ha eljutottunk egy levélig, akkor háromszög-sugár metszést kell vizsgálni.
Ha nem levélben vagyunk, akkor „sugár-altér” (bounding box) metszésvizsgálatot kell csinálni.
Mindkét háromszögre megkapjuk a „t” távolságokat. Nekünk a kisebb értékű „t” (háromszög) kell, számoljuk ki milyen textúra szín és fény éri azt a pontot, és tároljuk el azt a színt.
Ez a térfelosztás azért jó, mert, ha pl. 1millió háromszögből áll egy pálya, akkor az 1millióhoz képest kevés altér vizsgálattal eljutok a „nagy valószínűségű, hogy metsző” háromszögekig.
- Tegyük fel, hogy van 1millió háromszögem. Ha nem lenne térfelosztás, akkor egyesével, minden háromszöget vizsgálni kéne, ez 1 millió vizsgálat.
- De ha BVH segítségével keresünk, akkor kb. 100 vizsgálattal megkapom a metsző háromszögeket. Kevesebb így a háromszög metszéspont keresés vizsgálat.
Hogyan lehet egy háromszögek listából, BVH fát felépíteni?:
Adottak a háromszögek. Első lépésben veszek egy háromszöget, és megkeresem a hozzá legközelebbi másik háromszöget. „Csúcs-csúcs” vizsgálat elég, mert általában a felületek folytonosak, zártak mindig van egy háromszögnek egy olyan csúcsa, ami egy másik háromszöghöz is tartozik. Ebből a két szomszédos háromszögből, egy csomópontot lehet csinálni. A csomópontot egy „List<Node> nodes” listába teszem és a két háromszöget törlöm a „háromszögek listájából”. Majd veszem a következő háromszöget a háromszögek listájából, és ugyan ezt a „szomszéd keresés” algoritmust futtatom, majd a megszületett csomópontot hozzá fűzöm a „nodes” listához. Addíg keresem egy háromszög szomszédos háromszögeit, amíg vannak háromszögek a „triangles” listában. Előfordulhat, hogy csak egy háromszög maradt a listában, annak nem tudok szomszédot találni, így belőle egy olyan csomópontot hozok létre, aminek csak egy gyereke van.
a „nodes” listában, most sok kicsi altér van. Ezekkel az alterekkel ugyanúgy elvégezzük a szomszéd keresést, ugyan úgy, mint a háromszögeknél. Mindig, az újjonan keletkező csomópontokat bele tesszük egy új „List<Node> out” listába, majd ha az „List<Node> in” listából, ha elfogytak a csomópontok, akkor az „in = out; out = new List<Node>();” (az out lista az in listába kerül, és egy új, üres out Lista jön létre), és kezdődik elölről a szomszédok keresése.
Egyszer eljutunk egy olyan állapothoz, amikor az in Listában egy elem lesz. Az lesz a gyökér elem.
(Amikor létre hozunk egy csomópontot, akkor mindig kiszámoljuk a gyerekei altérből, az aktuális alteret, amiben mindkét gyerek altér benne van).
Így létre jön egy BVH fa.
Ez a gráf addig „jó”, amíg a háromszögek mozdulatlanok. De a számítógépes grafikában a háromszögek mozognak. Pl. animáció. Hogyan lehet egy már felépített fát, amiben, ha elmozdul egy háromszög (valamelyik csúcsa), akkor újra „jóvá” tenni? Lehet ezt párhuzamosan számolni? Igen. Az altereket (bounding boksz-okat) kell újra számolni.
A következő rész egy fa „újra jóvá tételét” mutatja be.
4.2.3 BVH gyors újra építése, ha a csúcsok megváltoztak:
Mi van akkor, ha egy BVH fa háromszögeinek csúcsai transzformálódott? Újra kell építeni az egész fát? Nem.
Két eset lehet:
- Animációkor, a háromszögek szomszédsága megmarad, pl. felemeljük a kezünket. Hagyományos animációkor ez az állítás érvényes.
- Animációkor a háromszögek szomszédsága nem marad meg, pl. levágják egy ember kezét, és messzire eldobják.
Én azt a megoldást választottam itt, hogy mindkét esetben a háromszögek szomszédságán nem változtatok a BVH-n belül.
Első esetben ez nem gond, a háromszögek szomszédsága ugyanúgy megmarad, csak az altereket kell a gyerekektől a szülők felé újra számolni.
Második esetben, „amikor messzire repül a kéz”, akkor is csak az altereket számoljuk újra, igaz ilyenkor nem lesz optimális a BVH bejárás, mert több 10 méter is lehet a távolsága a kéz és ember között, pedig biztosan lenne közelebbi háromszög.
Sajnos nem tudok megoldást, amivel gyorsan a háromszögek szomszédságát újra lehetne számolni. De ha a csomópont altereket újra számoljuk, függetlenül attól, hogy nem tökéletes a szomszédság, így is gyorsabb a fa bejárással, a metsző háromszögek keresése, mintha egyesével járnánk végig az összes háromszöget, metszéspontot keresve.
Megoldás: „ne szakadjon le a kéz”. Maradjon meg a szomszédsági viszony. De ez nem lehetséges (mindig).
Az altereket hogyan lehet párhuzamosan számolni?:
- tudjuk azt egy fa gráfról, hogy vannak szintjei. Én most megfordítom a szintek sorszámozását. Legyen a 0. szint a levelek, vagyis a háromszögek szintje. az 1. szint, a háromszögek szülői, … az N. szint pedig a gyökér.
- Tudjuk azt is, hogy egy pl. 5. szintet csak akkor tudom párhuzamosan számolni, ha a 4. szint alterei már kiszámításra kerültek.
Tehát a 0. szintű háromszögekből inicializáláskor készítek egy OpenCL „Buffer<Node> level0” buffert, ő egyben in/out buffer és kiszámolom a háromszögek altereit OpenCL-el. Így a 0. szint altereit kiszámolta az OpenCL, párhuzamosan, el lehet kezdeni az 1. szintű Node -k altereinek számolását. Fontos: Egy Node egyszerre altér és háromszög. Onnan tudom hogy egy Node levél (vagyis hogy háromszög), hogy nincs egy gyereke sem.
Minden szint egy „Buffer<Node>”. Ezt előfeldolgozási lépésben ki lehet számolni, hiszen egy BVH fa szintjei mindig ugyan azok maradnak, csak a levelek változnak.
Sorra kiszámolom a 2,3,4,5 … N -edik szintig párhuzamosan a szintek csomópontjainak altereit OpenCL-el, a gyerekek altereiből. Így frissítettem egy BVH fát.
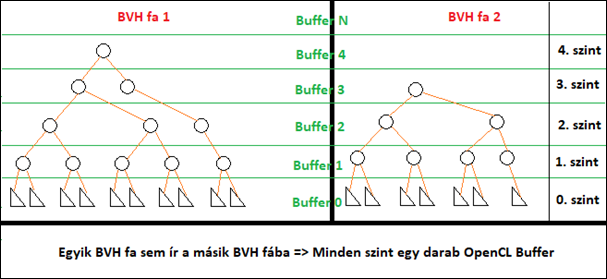
5. ábra: BVH fák szintjei. Egy szint elemei párhuzamosíthatók OpenCL-el [saját]
Sőt ahogy a kép is mutatja, ha sok BVH fa van, legyen mondjuk 2 darab (vagy több), vagyis több objektum van a világban. Amikor készítem pl. 0. szintet, akkor össze lehet fűzni mind a 2 darab 0.ás szintű level-eket, és egy nagy level0 Buffer keletkezik. Ugyanígy level N-ig. Mivel egyik BVH fa sem ír/olvas a másik BVH fa Node -jéből/-jébe, függetlenek egymástól, ezért összefűzhetők, párhuzamosíthatók.
Egy fa szintje, kb. 15-25 lehet. Ha kiszámoljuk, ha 25 szintű a fa, akkor elfér benne (2^25) 33 millió háromszög a levelekben, BVH-nként. És csak 25 darab OpenCL függvényhívást kellett a megfelelő sorrendben meghívni, akkor is, ha több BVH fa van, és újra „jóvá” tettük a fát.
Külömbséget kell tenni animált és nem animált BVH fa között. Az animált BVH fa „Dynamic” típusú, a nem animált BVH fa „Static” típusú. Elég csak a „Dynamic” típusú BVH-knak a altereit frissíteni. Azt hogy egy BVH fa Static vagy Dynamic lesz-e, azt a programozó dönti el. Egy Static típusú BVH-nak sohasem változnak meg a háromszög csúcsainak pozíciói, így azt elég egyszer, inicializáláskor az altekreket frissíteni.
Statikus BVH-nak számít a mozdulatlan pálya, míg Dynamic BVH-nak számít az animált-, vagy a térben máshová kerülő tárgyak.
Az OpenCL level1,2, .. 25 Bufferekbe csak a Dynamic típusú BVH fákat kell bele tenni.
5. Textúrázás Barycentrikus koordinátákkal:
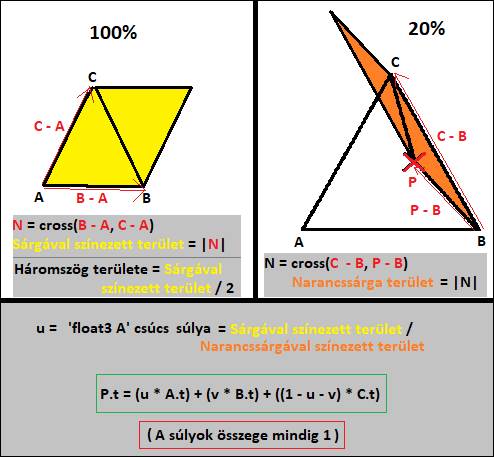
6. ábra: textúrakoordináta számítása, a P pontban [saját termék]
Ha ismerem az A-, B, és C csúcshoz tartozó textúra koordinátákat, és ki szeretném számolni a P metszéspont textúra koordinátáját, azt hogyan kell? Súlyokkal [18].
Képzeljük el, hogy ha egy P metszéspont közel van az A csúcshoz, akkor az A csúcs textúra koordinátához közeli értékű lesz a P csúcs textúra koordinátája. Minél messzebb kerül a P pont az A csúcstól, és minél közelebb kerül a B csúcs felé, annál inkább a B csúcs textúra koordinájához közeli értéket fog a P csúcs textúra koordinátája fel venni. Ugyan ez a C csúccsal.
Súlyokat kéne létre hoznom, amik megmondják [0.0 .. 1.0] intervallumban, hogy milyen közel vagyok egy csúcshoz. Ha nagyon közel vagyok pl. az A csúcshoz, akkor az A csúcs súlya 1.0-hoz közeli szám, és a B és C csúcsok súlya 0.0-hoz közeli szám. Az A csúcs textúra koordinátája fog jobban részt venni a P csúcs textúrakoordinátájának számítása közben, a B és C csúcsok, közel 0%-al fognak részt venni. A súlyok összege 1.0-et kell hogy kiadjon.
Hogyan tudom az A csúcs „float u” súlyát kiszámolni? Ahogyan a kép is mutatja, ha kiszámolom a teljes háromszög területét (A, B, C csúcsok), ez legyen „t1”. Majd, ha kiszámolom az A csúccsal szemközti (P, B, C csúcsok) háromszög területét, legyen ez „t2”. Majd „float u = t2 / t1”. Így egy kisebb számot osztok egy nagyobb számmal, pont az A csúcs súlyát fogom megkapni. A mellékelt ábra az A csúcs súlyának kiszámítását mutatja be.
Számoljuk ki a B csúcsal szemközti kis háromszög területét, ez legyen „t3”. Majs a súly: „float v = t3 / t1”. A C csúcs súlyát ugyan ezen elven lehet kiszámolni, de felesleges, mivel tudjuk hogy „u + v + w = 1”, ebből következik, hogy a C scsúcs súlya: „1 – u - v”.
Ismerjük a három súlyt, alkalmazzuk, ezt képletet: „P.t = (u * A.t) + (v * B.t) + ((1 – u - v) * C.t)”. Így megkapjuk a P pontban lévő textúra koordinátát. Ugyan ezzel a módszerrel, nem csak textúra koordinátát, hanem normálvektort, vagy pozíciót is lehet számolni. Hogyan kell kiszámolni egy háromszög területét? Ahogyan a kép is mutatja, egy A, B, C csúcsú háromszög területe egyenlő
„length(cross(B - A, C - A)) / 2.0”. „cross()” a vektoriális szorzat, „length()” a vektor hossza. És osztani kell kettővel.
6. Shaderek:
Az én alkalmazásomban, a címben szereplő 5 lépésre osztottam a futószalagot. Ezek OpenCL függvények.
6.1 TriangleShader:
A „TriangleShader” OpenCL függvény feladata, hogy a paraméterül kapott „Buffer<Node> inNodes” buffer háromszögeit frissítse. Ha az aktuális Node egy altér, (tehát nem háromszög), vagy ha a Node háromszög és „Static” típusú, akkor nincs szükség frissítésre, elég csak ezt a node-t átmásolni a ” Buffer<Node> outNodes” listába.
Különben, ha egy Node háromszög (levél), és „Dynamic” típusú (módosulnak a csúcspontjai a háromszögnek), akkor a háromszög A, B, C csúcsára meg kell hívni egyesével a „VertexShader” opencl fuggvényt, ami transzformálja (a térbe máshova helyezi) az A, B, C csúcsokat. Oda helyezi a csúcsokat a VertexShader, ahova a programozó szeretné. A VertexShader megvalósítása a programozó feladata. Ha ez megtörtént, akkor a TriangleShader újraszámolja az új háromszög területét.
6.2 VertexShader:
A „Vertex Shader”, ahogy fennt írtam, paraméterként egy darab csúcsot kap. Egy csúcs több változót tartalmaz: Csúcs pozíciója, a csúcshoz tartozó textúra koordináta, a csúcshoz tartozó normal vektor. Általában elég csak a csúcs pozícióját és normal vektor-ját transzformálni a „Vertex Shader” -ben, a textúra koordináta változatlan szokott lenni.
6.3 RefitTreeShader:
A „TriangleShader” OpenCL függvényhívás egy olyan „Buffer<Node> outNodes” fát ad eredményűl, amiben a levelek (háromszögek) kiszámításra kerültek (0. szint, valid). De a gráf felsőbb szintjei, vagyis az alterek nem valid-ak, azokat újra kell számolni. A „RefitTreeShader()” opencl függvény hívással lehet az altereket újra számolni. Fontos, hogy a „RefitTreeShader” függvényhívást előzze meg a „TriangleShader()” függvényhívás. Elég csak akkor meghívni a RefitTreeShader() függvényt, ha a világ rendelkezik „Dynamic” típusú objektummal (háromszöggel).
Ahogy feljebb írtam, a gráfokból, szintenként egy-egy „Buffer<Node> inoutLevelN” buffer létrehozható. Tehát „level0”, „level1” „level2” … kb „level25” buffer elég a gráfok tárolásához. A buffereket a megfelelő sorrendben kell meghívni. Először csak a háromszögeket tartalmazó „level0” buffer-t kell paraméterül átadni a „RefitTreeShader()” OpenCL függvénynek. A háromszöget tartalmazó buffer, a fák leveleit tartalmazza, nincsen egy Node csomópontnak egy gyereke sem, nem függ a Node-ben található altér, gyerekeitől, mert nincs gyereke a levélnek. Mivel nincs függőség, ezt a buffert lehet számolni. A „RefitTreeShader(level0)”-nek ezt a buffert átadva, frissíti az altereket (bounding box). Ha a „Buffer<Node> level0” alterei frissítve lettek, akkor a gráfban, az egyel felette lévő szintet (level1) lehet számolni, mert a „level1” alterek, csak az egy szinttel alatta lévő, (level0) alterektől függ. Hívjuk meg a „RefitTreeShader(level1)” függvényt, aminek paraméterül az 1. es szintet adjuk. Majd így folytatva, hívjuk meg a függvényt, paraméterként megfelelő sorrendben a 2., 3., … N. bufferekkel. Így a gráf Node-jeinek, alterei helyes értékeket tartalmaznak. Fontos, hogy ez a megoldás gyorsabb, mint ha CPU- val végeznénk egyesével a csomópontok altereinek újra számolását. A „RefitTreeShader()” OpenCL függvény párhuzamosan számolja a paraméterül kapott Node-ket, max. kb. 25 függvényhívással, míg CPU-n elvégezve, ez akár több ezer egymás utáni számítás is lehet.
Most világban lévő háromszög adatok validak.
6.4 GenerateCameraRays Shader:
Kamera pozícióból és látószögből sugarakat hoz létre ez az OpenCL függvény.
Ahhoz hogy a monitoron egy pixel színét megkapjuk, szükség van egy kiinduló sugárra, ami úgymond a monitor pixeléből indul, megkeresi a háromszögek között a legközelebbit, kiszámolja a színt, majd tükör-, és törési- irányba újabb sugarat indít, amivel szintén a legközelebbi háromszöget keresi, abból kiszámolja megint a metszéspontot érő fényt, majd újabb sugarakat indít tükröződési- törési- irányba, és így tovább. Úgy gondolom, elég 2x-3x egy képernyő pixeléből kiinduló sugárral új sugarakat generárni, és új színt keresni, mert ez gépigényes feladat még a videokártyának is.
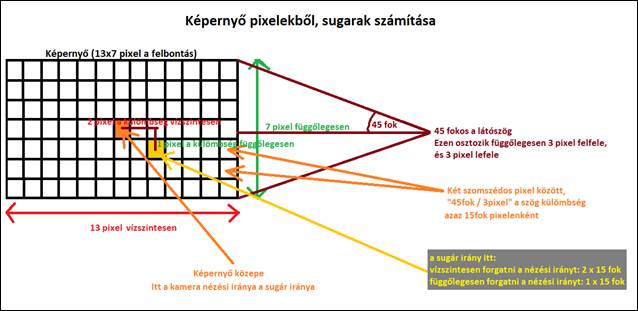
7. ábra: Képernyő pixelekből, sugarak előállítása [saját]
Tehát először is szükség van a monitor pixeleiből, kiinduló sugarakat létre hozni. Erre van a „GenerateCameraRays()” OpenCL függvényhívás.
Paraméterül megkapja a függvény egy felbontást (pl. 640x480), így tudni lehet, hogy mennyi sugarat kell létre hozni. Paraméterül kap még egy kamera pozíció és nézeti irányt. Ezekből az értékekből tudja a függvény, hogy a felbontás közepén lévő pixel-nek mi a kiinduló pontja és iránya. Ha 640x480 a felbontás, akkor a képernyő közepén (320x240. pixel) található sugár kiinduló pontja a kamera pozíciója, a sugár iránya pedig a kamera nézeti iránya. Tehát a képernyő közepén leévő sugár mindig meghatározható, minden egyes sugár létrehozáskor. Minden egyes pixelből ki lehet számolni, hogy hány pixel távolságra van a képernyő középpontjától (középpont: 320x240). Ha tudjuk a távolságot, akkor ha a képernyő közepén lévő sugár nézőpontját ennyivel eltoljuk, akkor lehet generálni bármelyik pixel-ből, sugarat.
Kérdés, hogy két szomszédos pixel között, mennyi a sugár nézeti pont eltolása? A programozó azt megadja, hogy a világot hány fokos látószögű kamerával szeretné nézni. (Az emberi 45fok-os szögben lát, ezt az értéket szokták használni általában a programozók). Ha a felbontás függőlegesen 480 pixelből áll, és tudjuk azt, hogy a képernyő közepe, vagyis a 240. pixelnél 0fok az különbség és és függőlegesen a 0. pixel -hez a 45fok tartozik, és függőlegesen a 480. pixelhez szintén a -45fok tartozik, akkor a függőlegesen a köztes pixelekhez [1 .. 239, 241 .. 479] lehet tudni hogy milyen fok tartozik hozzá.
A képernyő közepén lévő 0fokhoz tartozó kamera nézeti irányt most már tudjuk minden pixelre, hogy mennyivel kell elforgatni függőlegesen.
Ha tudjuk hogy 45fokon osztozik 240 pixel (640x480-as felbontáson), akkor két szomszédos pixel között, 45/240 elforgatás tartozik.
Ebből kiindulva ki lehet számolni a vízszintes [0 .. 640] pixelekhez tartozó elforgatást is.
Ha tudjuk hogy egy pixelhez mekkora szögelfordulások tartoznak, akkor a képernyő közepén lévő sugár irányát elforgatjuk ezekkel a fokokkal, így magkapjuk bármelyik pixel sugarának irányát. Minden képernyőből induló sugár kiindulópontja a kamera pozíciója.
A képernyő sugarakat egy „Buffer<ray> rays” bufferbe el kell tárolni, mert szüksége lesz a „RayShader”-nek ezekre.
A sugarak létrehozása egymástól nem függ, tehát ezeket is lehet párhuzamosan létre hozni. 640x480-as felbontás, 307200 pixelt tartalmaz, ekkora méretűre kell létre hozni a
„Buffer<ray> rays” buffert.
Egy 2D-s pixelből, 1D-s tömbbéli indexet, ezzel a képlettel kaphatunk:
int id = (width * y) + x; // (width, height) a képernyő felbontása, (x, y) egy tetszőleges pixel. Így az 1D-s tömbbe tudjuk írni a 2D-s pixelből létrehozott sugarat.
6.5 RayShader:
A ray shader eredménye egy szín. A klasszikus opengl2.0/direct3d9-nél a pixel színének kiszámítását a „pixel/fragment shader” nevű függvény végezte. Most ezt helyettesíti a „RayShader()”.
Régen csak a legközelebbi pixel pozícióját, és a fényforrásokat ismertük. Csak a fényforrásból érkező színnel lehetett egy pixel színét kiszámolni.
Sugárkövetésnél igaz, hogy a képernyőből induló sugarak és háromszögek metszéspontja ugyanúgy a képernyőhöz legközelebbi pontot adja eredményül. Szín számításkor ugyanúgy csak a fényforrások helyzetét vesszük csak számításba.
DE: sugárkövetésnél lehet folytatni a színszámítást [18].
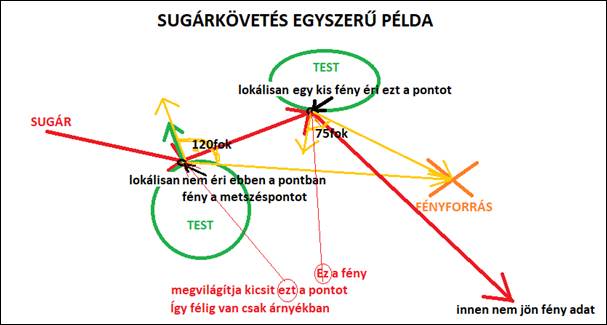
8. ábra: sugárkövetés példa (csak tükröződés van benne, törés nincs) [saját]
A sugár-háromszög metszéspontban, tükör irányba és/vagy törési irányba újabb sugarakat lehet indítani, ami, ha elmetsz egy másik háromszöget, akkor azzal a metszésponttal szintén ki lehet a számítani a fényforrások helyzetéből a metszéspontot érő színt. Ezt a színinformációt ismerve, az eredeti képernyő pixel színét lehet módosítani. Így lehet például olyat csinálni, hogy:
Első sugár indításkor, és fényforrás pozíció szerint árnyékban van a pont, tehát fény nem éri ezt a pontot. De ha tükröződeési- törési- irányba újabb metszéspontot keresünk, lehet, hogy az újabb metszéspontot éri a fény, ami megvilágítja az eredeti, fényt nem érő pontot. Tehát a fény most már tud pattogni, és olyan helyre is eljutni több pattogás közben, ami a kalsszikus opengl2.0/direct3d9 pixel shader-rel nem kiszámítható.
Az én megvalósításomban, a „RayShader()”-t is a programozó programozza. A RayShader függvény kap paraméterül egy „Hit *hits” ütközéspontokat tartalmazó listát, és egy sugarakat tartalmazó „Ray *rays” listát. Ezek a listák 2D-sak. Az első dimenzió a sugár hosszát mondja meg. Hányadjára tükröződik/törik egy pixelből indított sugár. A második dimenzióba több sugarat is tehetünk, több irányba folytathatjuk a sugárkövetést. A 2D-s tömb mérete [6][64]. tehát egy képernyőből induló sugár 6 hosszú lehet (első dimenzió), és lépésenként maximum 64 sugarat kezelhetek egyszerre (második dimenzió).
Ez a 2D-s tömb nem a legjobb megoldás, mert az 1. lépésben is lefoglalok a memóriában 64 sugárnak helyet, ami szinte biztos, hogy nincs kihasználva.
Azt az elméletet próbáltam követni, hogy: Ha minden lépésben 2 sugarat indítok (egyet tükröződési, egyet törési irányba), és minden sugár mindig ütközik háromszöggel, akkor a 6. lépésben, 2^6 = 64 különböző sugarat kell kezelnem. Tehát a 2D-s tömb (5. indexű) utolsó rekeszében kihasználom a maximum használható 64 sugarat. De az első vagy második lépésben valószínű, hogy nem kezelek 64 sugarat egyszerre.
A „8. ábra” azt mutatja, hogy egy pixel színének kiszámításához, 3 lépést használtam fel, és lépésenként 1 sugarat indítottam. Hogyis néz ez ki RayShader-ben? Paraméterként megkapom mindig a „hits”- és „rays” 2D-s tömböket. Ezeket így kell használni:
Első lépés: hits[0][0]-ba kerül a képernyő pixeléből kiinduló sugár, ezzel számolok. Ha ütközés van, akkor a „rays[1][0]”-ba helyezem a következő sugarat.
Második lépés: „hits[1][0]”-ban megkapom az előző lépésben, a „rays[1][0]”-ba elhelyezett sugár eredményét. Ha a „hits[1][0]” azt mondja hogy ütközés van, akkor a „rays[2][0]”-ba bele helyezem a következő sugarat.
Harmadik lépés: „hits[2][0]”-ban megkapom az előző lépésben, a „rays[2][0]”-ba elhelyezett sugár eredményét. Most a „hits[2][0]”, a kép alapján azt mondja, hogy nincs ütközés. Itt befejezem a sugár indításokat. Kiszámolom a „hits” 2D-s tömbben lévő ütközési pontokból és normal vektorokból, illetve a fényforrásból érkező színeket, összeadom őket, így kiszámoltam a pixel színét.
Ha a „RayShader”-ben false értékkel térek vissza, az azt jelenti, hogy nincs vége a pixel színének számításnak.
Így is fogalmazhatjuk: „új sugarat helyeztem a „Ray *rays” tömbbe, ha elmetsz háromszöget ez a sugár, akkor kérem a „Hit *hits” tömbben a metszéspontot. Majd hívódjon meg újra a RayShader() függvény”. Tehát a sugárkövetést folytatom.
Ha a „RayShader”-ben true értékkel térek vissza, az azt jelenti, hogy vége van a sugárkövetésnek.
Így is fogalmazhatjuk: „nem helyeztem új sugarat a „Ray *rays” tömbbe, kiszámoltam a „Hit *hits” adatokból az eredeti pixel színét, amit beírtam a paraméterként megkapott képernyő-textúrába”. A sugárkövetést befejezem ebben a pixelben.
7. Fények és árnyék számítása RayShader-ben:
Az alábbi képernyőkép (9. ábra) mutatja, hogy hogyan néz ki a RayShader eredménye, aminek a megírása a programozó feladata. Amit lejjebb bemutatok algoritmust, annak eredménye (9. ábra) ez a kép:

9. ábra: diffúz színek és árnyékok, RayShader-ben [saját]
Nulladik lépés: A képernyőképet törlöm. Jelen esetben ez a kék szín.
Első lépés: Megkapom RayShader-ben, a „hits[0][0]”-ban, hogy egy pixelben lévő sugár elmetsz-e egy háromszöget. Ha nem metsz el egy háromszöget sem, akkor befejezem a pixel színének számítását „return true” visszatérési értékkel. Ha van háromszög metszés, akkor az aktuális pixelt feketére színezem, mert ezt a pixelt még nem éri fény. A valóságban is így van ez. Illetve én három fényforrást hozok létre, amik messze vannak, a megvilágítandó objektumtól, így „irány fényforrás” hatást lehet elérni. Kiszámolom a három fényforrás pozícióból és az aktuális pixel metszéspontból, a három sugarat, amit bele helyezek a „rays[1][0]”, „rays[1][1]”, és „rays[1][2]”-be. Majd azt mondom a RayShader-nek, hogy „return false” (nincs vége a szín számításnak, kérem az 1.es rekeszbe tett sugarak metszéspontjait).
Második lépés: a „hits[1][0]”, „hits[1][1]” és „hits[1][2]” megmondja, hogy a három fényforrásból induló sugár metsz-e el háromszöget. Mi a fényforrás szemszögéből, a legközelebbi háromszög metszéspont. (Fontos: most egy pixel színét számolom) Ha nincs metszéspont, akkor „return true”-val befejezem a pixel színének számítását. Nem írok a képernyő textúrába semmit, tehát az a pixel, változatlan marad, ez a fényforrás, ezt a pixelt nem világítja meg (de lehet, hogy pl. a 2. vagy 3. fényforrás megvilágítja?).
Onnan lehet tudni hogy egy pixel metszéspontját éri-e fény, vagyis hogy nincs árnyékban, hogy a fényforrásból indított sugár, ugyan azt a metszéspontot adja eredményül, mint amit a képernyőből indított sugár talált metszéspontot.
Onnan tudom hogy a két pont különbözik-e egymástól, hogy a két pont távolsága túl nagy egymáshoz képest (a nagy távolság árnyékot jelent). Azokat a pixeleket, amiket fény ér, kiszámolom a diffúz színüket, mindhárom fényforrásra, összeadom őket, bele írom az új színt a képernyő textúra pixelébe. Majd (én) „return true”-t mondok, tehát befejezem az aktuális pixel színének számítását.
A fent leírt eljárás, a (9. ábra) képet adja eredményül.
„Hello World” példakód a VertexShader-re:
Vertex VertexShader(Vertex in, __global Matrix4x4 *in_Matrices)
{
Vertex out;
out = in;
if (1 == in.numMatrices)
{
float3 v1 = Mult_Matrix4x4Float4(in_Matrices[in.matrixId1], ToFloat4(in.vx, in.vy, in.vz, 1.0f);
out.vx = v1.x;
out.vy = v1.y;
out.vz = v1.z;
float3 n1 = Mult_Matrix4x4Float4(in_Matrices[in.matrixId1], ToFloat4(in.nx, in.ny, in.nz, 0.0f);
float3 n = normalize(n1);
out.nx = n.x;
out.ny = n.y;
out.nz = n.z;
}
else if (2 == in.numMatrices)
{
;
}
else if (3 == in.numMatrices)
{
;
}
return out;
}
Ez a kód új pozícióba helyezi az „out.v” -t, és elforgatja az új irányba az „out.n” -t, egy mátrix segítségével [19].
„Hello World” példakód RayShader-re:
bool RayShader(Hits *hits, Rays *rays, __global Material *materials, __global unsigned char *textureDatas, __global unsigned char *out, int in_Width, int in_Height, int pixelx, int pixely)
{
if (hits->id == 0)
{
Hit hit = hits->hit[hits->id][0];
if (hit.isCollision == 0) { return true; }
Color textureColor = Tex2DDiffuse(materials, textureDatas, hit1.materialId, hit1.st);
Color diffuseColor;
diffuseColor.red = float)textureColor.red;
diffuseColor.green = float)textureColor.green;
diffuseColor.blue = float)textureColor.blue;
diffuseColor.alpha = 255;
WriteTexture(out, in_Width, in_Height, ToFloat2(pixelx, pixely), diffuseColor);
return true;
}
return true;
}
Ez a kód, ha „id == 0”, akkor fut le.
Ha nincs ütközés háromszöggel, akkor „return true”, vége a sugárkövetésnek, nem módosítunk az aktuális pixel színén.
Ha van ütközés háromszöggel, akkor lekérdezzük a a textúra színét, amit elmetsz a sugár, majd ezt a színt bele írjuk a textúrába, és „return true” -val vége a sugárkövetésnek.
Még egy példa, árnyékok és tükröződés számítására, RayShaderben:
Egy példa kódot szeretnék bemutatni, ami a RayShader használatát mutatja be. Létrehozok 3 fényforrást, amik diffúz színt számolnak (árnyékkal), illetve egy tükröződést mutatok be [18][19]:
A kép:
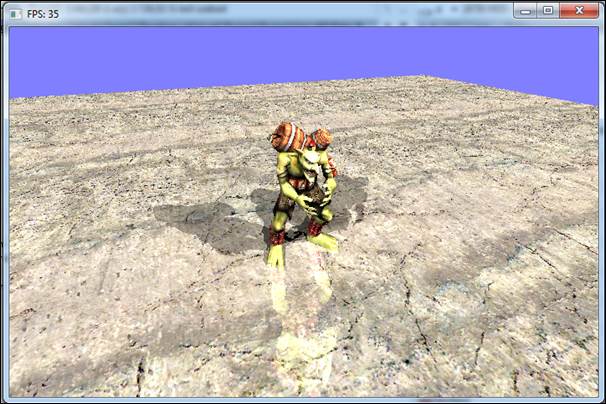
10. ábra: árnyék és tükröződés példa [saját]
A forráskód:
bool RayShader(Hits *hits, Rays *rays, Vector3 camPos, Vector3 camAt, __global Material *materials, __global unsigned char *textureDatas, __global unsigned char *out, int in_Width, int in_Height, int pixelx, int pixely)
{
float3 light1; /*első fényforrás pozíciója*/
light1.x = +1000.0f;
light1.y = +1000.0f;
light1.z = +1000.0f;
float3 light2; /*második fényforrás pozíciója*/
light2.x = -1000.0f;
light2.y = +1000.0f;
light2.z = +1000.0f;
float3 light3; /*harmadik fényforrás pozíciója*/
light3.x = 0.0f;
light3.y = +1000.0f;
light3.z = +1000.0f;
float3 cam_pos;
cam_pos.x = camPos.x;
cam_pos.y = camPos.y;
cam_pos.z = camPos.z;
if (hits->id == 0)
{
/*első lépésként ha nincs ütközés, akkor rayshader leállítása*/
Hit hit = hits->hit[hits->id][0];
if (hit.isCollision == 0) { return true; } /*nincs ütközés, vége*/
/*fényforrások pozíciójából, sugár indítása, egy pixel felé*/
Ray newRay1; // light1
newRay1.posx = light1.x;
newRay1.posy = light1.y;
newRay1.posz = light1.z;
float3 dir1 = normalize(hit.pos - light1);
newRay1.dirx = dir1.x;
newRay1.diry = dir1.y;
newRay1.dirz = dir1.z;
newRay1.length = 5000.0f;
Ray newRay2; // light 2
newRay2.posx = light2.x;
newRay2.posy = light2.y;
newRay2.posz = light2.z;
float3 dir2 = normalize(hit.pos - light2);
newRay2.dirx = dir2.x;
newRay2.diry = dir2.y;
newRay2.dirz = dir2.z;
newRay2.length = 5000.0f;
Ray newRay3; // light3
newRay3.posx = light3.x;
newRay3.posy = light3.y;
newRay3.posz = light3.z;
float3 dir3 = normalize(hit.pos - light3);
newRay3.dirx = dir3.x;
newRay3.diry = dir3.y;
newRay3.dirz = dir3.z;
newRay3.length = 5000.0f;
/*tükröződés irányba sugár indítása. ez a negyedik sugár ebben az első lépésben*/
Ray newRay4; // reflection
float3 pos = hit.pos + hit.normal * 0.01f;
newRay4.posx = pos.x;
newRay4.posy = pos.y;
newRay4.posz = pos.z;
float3 dir4 = reflect(normalize(hit.pos - cam_pos), hit.normal);
newRay4.dirx = dir4.x;
newRay4.diry = dir4.y;
newRay4.dirz = dir4.z;
newRay4.length = 5000.0f;
rays->id = 1;
rays->count[rays->id] = 4;
rays->ray[rays->id][0] = newRay1;
rays->ray[rays->id][1] = newRay2;
rays->ray[rays->id][2] = newRay3;
rays->ray[rays->id][3] = newRay4;
return false;
}
/*második lépés*/
if (hits->id == 1)
{
/*ha az első lépésben nem volt metszéspont, akkor kilépés*/
Hit hit1 = hits->hit[0][0];
if (hit1.isCollision == 0) { return true; }
/*alapértelmezésben a pixel diffúz színének intenzitása, 0*/
float diffuseIntensity = 0.0f;
Hit hit2 = hits->hit[hits->id][0];
if (hit2.isCollision == 1)
{
float length2 = length(light1 - hit2.pos);
float length1 = length(light1 - hit1.pos);
/*első fényforrás: ha nem vagyunk árnyékban, akkor az aktuális pixel diffúz színének számítása*/
if ((length2 + 0.005f) > length1)
{
float3 dir = normalize(hit1.pos - light1);
diffuseIntensity += max(dot(-dir, hit2.normal), 0.0f);// + max(dot(-dir2, hit.normal), 0.0f);
}
}
/*második fényforrás: ha nem vagyunk árnyékban, akkor az aktuális pixel diffúz színének számítása*/
Hit hit3 = hits->hit[hits->id][1];
if (hit3.isCollision == 1)
{
{
float length2 = length(light2 - hit3.pos);
float length1 = length(light2 - hit1.pos);
if ((length2 + 0.005f) > length1)
{
float3 dir = normalize(hit1.pos - light2);
diffuseIntensity += max(dot(-dir, hit3.normal), 0.0f);
}
}
}
/*harmadik fényforrás: ha nem vagyunk árnyékban, akkor az aktuális pixel diffúz színének számítása*/
Hit hit4 = hits->hit[hits->id][2];
if (hit4.isCollision == 1)
{
{
float length2 = length(light3 - hit4.pos);
float length1 = length(light3 - hit1.pos);
if ((length2 + 0.005f) > length1)
{
float3 dir = normalize(hit1.pos - light3);
diffuseIntensity += max(dot(-dir, hit4.normal), 0.0f);
}
}
}
Color textureColor = Tex2DDiffuse(materials, textureDatas, hit1.materialId, hit1.st);
/*textúra szín és intenzitás beírása az aktuális pixelbe */
// diffuse
Color diffuseColor;
diffuseColor.red = (int)(((float)textureColor.red ) * diffuseIntensity);
diffuseColor.green = (int)(((float)textureColor.green) * diffuseIntensity);
diffuseColor.blue = (int)(((float)textureColor.blue ) * diffuseIntensity);
diffuseColor.alpha = 255;
// reflection
Hit hit0 = hits->hit[0][0];
Hit hit5 = hits->hit[hits->id][3];
if (hit5.isCollision == 1 && hit0.objectId == 0)
{
/*tükröződés: ha van metszéspont, ami a 0. objektumot metszi (vagyis a talajt), akkor színszámítás*/
Color reflectionColor = Tex2DDiffuse(materials, textureDatas, hit5.materialId, hit5.st);
float reflectionIntensity = diffuseIntensity * 0.25;
diffuseColor.red += (int)(((float)reflectionColor.red ) * reflectionIntensity);
diffuseColor.green += (int)(((float)reflectionColor.green) * reflectionIntensity);
diffuseColor.blue += (int)(((float)reflectionColor.blue ) * reflectionIntensity);
diffuseColor.alpha = 255;
}
WriteTexture(out, in_Width, in_Height, ToFloat2(pixelx, pixely), diffuseColor);
/*vége a sugár követésnek, ebben a pixelben*/
return true;
}
return true;
}
8. A ’class Scene’ osztály feladata:
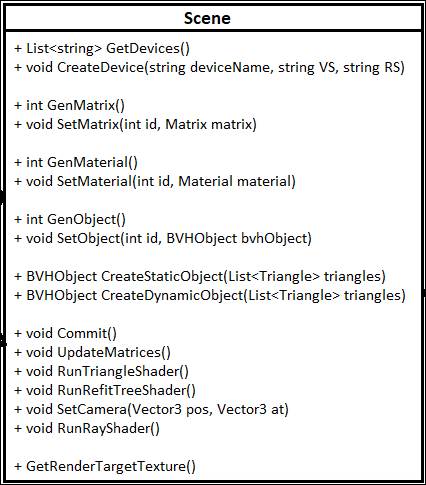
11. ábra: Scene osztály feladatai [saját]
A Scene osztály feladatai:
- A számítógépben lévő OpenCL eszközök kilistázása. Ehhez a "GetDevices()" függvényt lehet használni, ami visszatér egy listával, hogy milyen OpenCL eszközöket talált a rendszer.
- Egy OpenCL eszköz betöltése. Ki kell választani egy OpenCL eszközt a listából, és azon az eszköz fogja számolni a OpenCL függvény hívásokat.
- Matrix létrehozása, eltárolása, amit majd később el lehet érni. Egy OpenCL Bufferben létrejön egy mátrix, amit majd VertexShader-ben el lehet érni.
- Material (textúra) létrehozása, eltárolása, amit majd később el lehet érni OpenCL-el, a RayShader-ben.
- ’BVHObject’ objektum (statikus vagy dinamikus) létrehozása háromszög listából, és eltárolása, amit majd később el lehet érni OpenCL-ben a RayShader-ben.
- OpenCL parancsok kiadása (ezeket már bemutattam), amivel a végső kép elkészül, amit a képernyőre lehet rajzolni. Ezek a parancsok:
o void Commit()
o void UpdateMatrices()
o void RunTriangleShader()
o void RunRefitTreeShader()
o void SetCamera(Vector3 pos, Vector3 at)
o void RunRayShader()
- A végső, elkészült kép lekérése.
Az ’OBJLoader’ és ’SMDLoader’ osztályok feladata, hogy szabványos .obj vagy .smd fájlból, háromszög listatát, mátrixokat hozzanak létre, amivel már ’BVHObject’-et lehet létre hozni. Most ezeknek a fájloknak a betöltését mutatom be.
8.1 Statikus objektum betöltése, ’class OBJLoader’ osztály segítségével:
Az .OBJ fájl viszonylag elterjedt, minden 3D-s szerkesztőben megtalálható [22]. Ez a fájl nem támogatja az animációt. Az .OBJ mellett általában szokott lenni egy .MTL fájl is, amely a textúrákat és az anyagok tulajdonságait írja le.
Az alábbi kulcsszavak szerepelnek egy .OBJ fájlban:
· Megjegyzés:
# ez egy sornyi megjegyzés a fájlban, nem kerül értelmezésre
· Egy csúcspont:
v 2.963193 1.167374 -0.431719
Ha v szöveggel kezdődik egy sor, akkor utána három lebegőpontos szám következik, amelyek egy pontot adnak meg a térben. Ezeket gyűjtsük össze egy List<Vector3> vertices; listába.
· Egy textúra koordináta:
vt 0.875000 0.035000
Ha vt szöveggel kezdődik egy sor, akkor utána két lebegőpontos szám következik, amelyek egy textúra-koordinátát adnak meg. Ezeket gyűjtsük össze egy List<Vector2> textcoords; listába.
· Egy normál vektor:
vn 0.704114 0.480790 0.522556
Ha vn szöveggel kezdődik egy sor, akkor utána három lebegőpontos szám következik, amelyek egy, a felületre merőleges vektort adnak meg. Ezeket is gyűjtsük össze egy List<Vector3> normals; listába.
· Háromszögek:
f 1/2/3 1821/1924/2 609/712/3
Ha f szöveggel kezdődik egy sor, akkor utána szóközökkel elválasztva minimum három vertex következik. Az első vertex 1/2/3 jelentése: Az aktuális csúcs az 1. elem a vertices listából, a csúcshoz tartozó textúra-koordináta a 2. elem a textcoords listából, és a csúcshoz tartozó normálvektor a 3. elem a normals listából. Ne felejtsük el, hogy a lista indexelése 0-tól kezdődik, tehát az 1/2/3 azt jelenti, hogy egy vertex így néz ki:
class Vertex
{
public Vector3 v = vertices[0];
public Vector2 vt = textcoords[1];
public Vector3 n = normals[2];
}
Így van egy vertexünk [20]. Egy háromszöghöz három vertex kell. Ha több vertex szerepel egy sorban, akkor a 4. vertex a 3. és az 1. vertexszel alkot egy háromszöget. Az 5. vertex a 4. és az 1. vertexel alkot egy háromszöget, és így tovább.
· Materiál kijelölése:
usemtl Texture_0
Ha usemtl szöveggel kezdődik egy sor, akkor az utána szereplő materiál-azonosítóval úgymond megmondom, hogy a most következő f-ekre (háromszögekre) ezt a textúrát kell ráhúzni.
· Textúrák és tulajdonságaik:
mtllib cottage.mtl
Ha mtllib szöveggel kezdődik egy sor, akkor utána az .MTL materiálfájl neve szerepel, amely a textúrákat és azok tulajdonságait írja le. Az .MTL fájlban a legfontosabb kulcsszavak az alábbiak:
o newmtl Texture_0: Új materiált hoz létre, amelyre a Texture_0 névvel hivatkozhatunk. Most ez az aktuális materiál.
o mmap_Kd alma.bmp vagy map_Kd alma.bmp: Az aktuális materiál textúrája az alma.bmp. Ez nem mindig szerepel.
Kd 1.0 0.5 0.0: Az aktuális materiál színe red: 1.0, green: 0.5, blue: 0.0. Ha nincs textúra, akkor a színt kell használni.
.OBJ fájl kirajzolása OpenGL-el [20]:
foreach(Material material in materials)
{
glBindTexture(GL_TEXTURE_2D, material.texture_id);
glBegin(GL_TRIANGLES);
foreach(Vertex vertex in material.vertices)
{
Vector3 v = vertex.v;
Vector2 tc = vertex.tc;
Vector3 n = vertex.n;
glTexCoord2f(tc.X, tc.Y);
glNormal3f(n.X, n.Y, n.Z);
glVertex3f(v.X, v.Y, v.Z),
}
glEnd();
}
8.2 Dinamikus objektum betöltése, „class SMDLoader” osztály segítségével:
Az .SMD kiterjesztésű fájlt a Valve Corporation, 1996-ban alapított, videojátékokat fejlesztő amerikai vállalat hozta létre [23]. A Half-Life 1-2 Half-Life tudományos-fantasztikus belső nézetű lövöldözős (First Person Shooter, FPS) számítógépes játék is ezeket használja ahhoz, hogy animált modelleket jelenítsen meg.
Ez az .SMD kiterjesztésű fájl egy szöveges fájl. Két féle .SMD fájl létezik. Az egyikben mozdulatlan geometriát tárolunk (háromszögek), míg a másik típusban csak az animációt tároljuk. Mind a két féle fájlnak a kiterjesztése .SMD.
Miért kell külön tárolni a geometriát a hozzá tartozó animáció(k)tól? Azért, mert ha mi csak például a „futás” animációt szeretnénk betölteni, akkor elég csak ezt az egy animációt betölteni. Ha egy fájlban lenne a geometria és az összes animáció, akkor olyan animációt is betöltene a program, amelyre nincs szükség. Így tudunk válogatni, hogy mit töltsünk be, és mit ne.
Legelőször a geometriát kell betölteni – ezt kötelező. Utána töltjük be az animáció(ka)t. A geometriát tartalmazó fájlt szokás Reference.smd-nek nevezni, míg az animáció(kat)t tartalmazó fájl(oka)t pedig például Anim.smd-nek. Az .SMD kiterjesztésű fájl létrehozható 3D-s szerkesztőprogramokkal, például MilkShape3D-vel, 3DStudioMaxszal vagy Blenderrel (ehhez be kell kapcsolni a pluginját).
Az alábbi kódban példát látunk a Reference.smd fájl tartalmára:
version 1
nodes
0 "joint1" -1
1 "joint2" 0
2 "joint3" 1
end
skeleton
time 0
0 -0.750000 0.000000 0.500000 1.577046 0.000000 1.570796
1 0.000000 0.000000 40.000790 0.013222 0.000300 3.141593
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
end
triangles
Kep1.bmp
0 19.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 0.000000 1.000000
0 19.250000 -20.500000 -20.500000 0.000000 -1.000000 0.000000 0.000000 0.000000
0 60.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 1.000000 1.000000
Kep1.bmp
0 19.250000 -20.500000 -20.500000 0.000000 -1.000000 0.000000 0.000000 0.000000
0 60.250000 -20.500000 -20.500000 0.000000 -1.000000 0.000000 1.000000 0.000000
0 60.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 1.000000 1.000000
end
Az alábbi kód példa az Anim.smd fájl tartalmára:
version 1nodes0 "joint1" -11 "joint2" 02 "joint3" 1endskeletontime 00 -0.750000 0.000000 0.500000 1.577046 0.000000 1.5707961 0.000000 0.000000 40.000790 0.013222 0.000300 3.1415932 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000time 10 -0.750000 0.000000 0.500000 0.791647 0.000000 1.5707961 -0.000000 -0.000003 40.000549 0.798618 0.000212 -3.1413802 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000time 20 -0.750000 0.000000 0.500000 0.006249 0.000000 1.5707961 -0.000000 -0.000002 39.999920 1.584001 0.000000 -3.1412922 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000end
.SMD fájlok kulcsszavai
Az alábbiakban az .SMD fájlok kulcsszavait mutatom be.
· nodes: Jelentése csomópontok. A csomópontok felsorolása end-ig tart.
nodes
0 "joint1" -1
1 "joint2" 0
2 "joint3" 1
end
Minden sor egy csomópont. Például 1 "joint2" 0 jelentése: ennek a csomópontnak az azonosítója: 1, neve: joint2, a szülejének azonosítója: 0. Célszerű tömbben (listában) tárolni ezeket az adatokat. Ha az i. azonosítójú elemre vagyunk kíváncsiak, akkor a nodes[i] visszaadja az i. azonosítójú csomópont adatait. Ha a szülő azonosítója -1, azt jelenti, hogy ennek a csomópontnak nincs szülője, tehát ez a csomópont a gyökér. Fel lehet rajzolni fagráfban ezeket a csomópontokat, hiszen szülő–gyerek kapcsolat van a csomópontok között.
class Node
{
public:
string name;
public int parent_id;
};
List < Node > nodes;
· bone: Jelentése csont. Egy modell, például az ember mozgatásához csontvázrendszer van létrehozva. Ha mozgatjuk például a törzsünket, akkor vele mozog a hozzá kapcsolt fejünk, karunk. Tehát a csontok között hierarchia van, szülő–gyerek kapcsolat. Sok csont határoz meg egy csontvázat, angolul skeletont. Egy csont lokális transzformációval forogni tud az X, Y, Z tengelyek mentén, és eltolható a szülejéhez képest. Az alábbi kódrészletek egy csontra és egy csontvázra adnak példát.
// egy csont
class Bone
{
// lokális transzformációk. Eltérés a szülőhöz képest
public Vector3 translate;
public Vector3 rotate;
};
// egy csontváz csontok listájából áll
class Skeleton
{
public:
public List < Bone > bones;
};
Illetve egy animáció sok csontvázból áll:
// egy animáció
class Animation
{
public string name; // az aktuális animáció neve (Anim.smd)
public float fps; // 1 sec alatt, hány skeleton játszódik le
public List < Skeleton > times;
};
// sok animáció egy listában
List < Animation > animations;
· time: Jelentése idő.
time 0
0 -0.750000 0.000000 0.500000 1.577046 0.000000 1.570796
1 0.000000 0.000000 40.000790 0.013222 0.000300 3.141593
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
Az animációban vannak a csomópontok (csontok) lokális transzformációi. Például a 0 1.0 2.0 3.0 4.0 5.0 6.0 jelentése: a 0. csomópont lokális mátrixa ez:
Matrix4 local = Matrix4.Translate(1.0, 2.0, 3.0) * Matrix4.RotateXYZ(4.0, 5.0, 6.0);
Vagyis forgatás a tengelyek mentén 4.0, 5.0, 6.0 radiánnal, majd eltolás 1.0, 2.0, 3.0 egységgel. Ha egy modellben például 25 csomópont van, akkor egy time-ban 25 db transzformáció van felsorolva egymás után. Egy time egy pillanatot ábrázol. Ahhoz hogy ebből animáció legyen, ahhoz sok time kell egymás után. 1 másodperc alatt kb. 4-30 time jeleik meg a képernyőn. Két time között kb. 0,2 másodperc telik el. A két time közötti pillanatnyi eltolást lineáris interpolációval, a forgást előjeles szögelfordulással lehet kiszámolni:
times[0].bones[0].translate = new Vector3(1,0,0);
times[0].bones[0].rotate = new Vector(1,0,0);
times[1].bones[0].translate = new Vector(2,0,0);
times[1].bones[0].rotate = new Vector(2,0,0);
Ha például t = 0.2 (t = [0.0 .. 1.0]), akkor a pillanatnyi transzformáció ez [18]:
float t = 0.2;
current_skeleton.bones [0].translate = (times[0].bones[0].translate * (1 - t)) + (times[1].bones[0].translate * t); // lineáris interpoláció
// rotate X
float rotate_x = GetSignedRad(times[0].bones[0].rotate.X, times[1].bones[0].rotate.X);
current_skeleton.bones[0].rotate.X = start.bones[0].rotate.X + (rotate_x * dt);
// rotate Y …
// rotate Z …
Forgásnál fontos, hogy merre forgatunk. Például ha a kezdő szög 0,1 radián, a vég szög pedig 6,27 radián, akkor -0,2 radiánnal kell forogni az óra járásával megegyező irányba. Itt nem lehet lineáris interpolációval számolni, mert 6,26 radiánnal forogna az óra járásával ellentétes irányba.
· skeleton: Jelentése csontváz. time-ok vannak benne end végjelig:
skeleton
time 0
0 -0.750000 0.000000 0.500000 1.577046 0.000000 1.570796
1 0.000000 0.000000 40.000790 0.013222 0.000300 3.141593
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
time 1
0 -0.750000 0.000000 0.500000 0.791647 0.000000 1.570796
1 -0.000000 -0.000003 40.000549 0.798618 0.000212 -3.141380
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
time 2
0 -0.750000 0.000000 0.500000 0.006249 0.000000 1.570796
1 -0.000000 -0.000002 39.999920 1.584001 0.000000 -3.141292
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
end
Például egy time 0 leírja a 0. időben a csomópontok transzformációit, vagyis az aktuális csontváz csontjainak helyét és forgási szögeit. A Reference.smd fájlban csak egy time szerepel, ez a kezdeti beállása a modellnek. Míg az Anim.smd fájlban sok time szerepel, mindegyik leírja hogy az i. time-ban mi az aktuális csontváz, vagyis az aktuális transzformációk.
Egy csomópontnak úgy tudjuk kiszámolni a globális koordináta-rendszerben a transzformációját a lokális transzformációból, hogy vesszük a lokális transzformációt, majd rekurzívan összeszorozzuk a szülejének a lokális transzformációjával, azután a szülő szülejének a lokális transzformációjával addig, amíg el nem jutunk a gyökérig. A gyökér csomópont transzformációja az egység mátrix.
Itt egy példakód erre [18]:
Matrix4 GetMatrix(int bone_id)
{
if (bone_id == -1) return Matrix4.Identity;
// lokális transzformáció. Eltérés a szülőhöz képest
Vector3 r = currBones[bone_id].rotate;
Vector3 t = currBones[bone_id].translate;
Matrix4 local = Matrix4.Translate(t.X, t.Y, t.Z) * Matrix4.RotateXYZ(r.X, r.Y, r.Z);
// szülő transzformáció kiszámítása, rekurzívan
Matrix4 parent = GetMatrix(nodes[bone_id].parent_id);
// visszatérünk az aktuális transzformációval
return Matrix4.Mult(parent, local);
}
· triangles: A triangle jelentése háromszög poligon. Háromszögek felsorolva end végjelig. Egy háromszög így néz ki:
texture.bmp
1 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
2 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
3 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
Ez azt jelenti, hogy erre a háromszögre a texture.bmp-t kell illeszteni. Utána szerepel három sor. Minden sor egy csúcsot ír le. Az első sor ez: 1 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0. Ez azt jelenti, hogy a háromszög egyik csúcsa [1.0, 2.0, 3.0], normálvektora [4.0, 5.0, 6.0], textúra-koordinátája [7.0, 8.0]. Az első szám az 1-es azt jelenti, hogy ehhez a csúcshoz az első indexű csomópont tartozik. Így már hozzá van rendelve egy csúcs egy transzformációhoz.
Amikor animációt akarunk megjeleníteni, elég csak kiszámítani a pillanatnyi transzformációkat, majd a megfelelő csúcsokra alkalmazni.
Animáció kiszámítása és megjelenítése, OpenGL segítségével:
Végigjárjuk a materials listát, kijelöljük az aktuális textúrát, majd a material minden egyes csúcspontját transzformáljuk, majd kirajzoljuk OpenGL segítségével [18][19][20]:
void Draw()
{
glPushMatrix();
for(int i = 0; i < materials.Count; i++)
{
Material mat = materials[i];
glBindTexture(gl.GL_TEXTURE_2D, mat.texture_id);
glBegin(GL_TRIANGLES);
for(int j = 0; j < mat.vertices.Count; j++)
{
Vertex in = mat.vertices[j];
Matrix4 T = transform[in.id] * transformInverse[in.id]; // transzformáció kiszámítása
Vector3 v = T * Vector4(in.position, 1);
Vector3 n = T * Vector4(in.normal , 0); // itt nincs eltolás, csak forgás van
Vector3 t = in.texCoord;
glTexCoord2f(t.X, t.Y);
glNormal3f(n.X, n.Y, n.zZ);
glVertex3f(v.X, v.Y, v.Z);
}
glEnd();
}
glPopMatrix();
}
Mit is jelent a kirajzolásnál az alábbi sor?
Matrix4 T = transform[in.id] * transformInverse[in.id]; // transzformáció kiszámítása
Ez azt jelenti, hogy két listánk van. Egy List < Matrix4 > transform; és egy List < Matrix4 > transformInverse;.
A transform lista a pillanatnyi csontváz transzformációit tartalmazza. Ezt minden képkockán (frame-en) ki kell számítani [23]:
for(int i = 0; i < currBones.size(); i++)
{
transform[i] = GetMatrix(i);
}
A transformInverse lista pedig a Reference.smd fájlban található egyetlen csontváz transzformációinak inverzét tartalmazza. Ez mit is jelent? A Reference.smd fájlban található egyetlen csontváz adott, és a csúcspontok is adottak. Nevezzük el a Reference.smd fájlban található csontváz i. transzformációját T-nek, és a Reference.smd fájlban található egyik háromszög egyik csúcsát out-nak. Ha elképzeljük, akkor: Vector3 out = T * ?; Tehát adott az out vektor és a T mátrix a Reference.smd fájlban. A ? az ismeretlen, amire szükségünk lesz, ezért ki kell számítani.
Amikor a pillanatnyi animációt akarom megjeleníteni, akkor azt így kell: Vector3 v = transform[i] * ?;
Tehát fejezzük ki a ?-et: Vector3 out = T * ?; // átalakítás (fejezzük ki a ?-et)
1. egyenlet: Vector3 ? = Matrix4.Inverse(T) * out;
Ha megvan a ?, akkor:
2. egyenlet: Vector3 v = transform[i] * ?;
Egybe a két egyenlet: Vector3 v = transform[i] * inverse(T) * out; Így Vector3 v az aktuális animáció egyik csúcspontja.
Ezért szerepel a Draw() metódusban a fenti megoldás.
A transformInverse listát elég egyszer kiszámítani, például a Reference.smd fájl betöltése után [18]:
Matrix4 GetRefMatrix(int bone_id)
{
if (bone_id == -1) return Matrix4.Identity; // egységmátrix, ha a gyökérben vagyunk
// lokális transzformáció. Eltérés a szülőhöz képest
Vector3 r = referenceSkeleton.bones[boneId].rotate;
Vector3 t = referenceSkeleton.bones[boneId].translate;
Matrix4 local = Matrix4.Translate(t.X, t.Y, t.Z) * Matrix4.RotateXYZ(r.X, r.Y, r.Z);
// szülő transzformáció kiszámítása, rekurzívan
Matrix4 parent = GetRefMatrix(nodes[bone_id].parent_id);
// visszatérünk az aktuális transzformációval
return Matrix4.Mult(parent, local);
}
for(int i = 0; i < referenceSkeleton.bones.Count; i++)
{
transformInverse[i] = Matrix4.Inverse(GetRefMatrix(i));
}
A SetTime(float time) metódusban pedig a pillanatnyi csontvázat kell kiszámolni, amelyet majd később kirajzolunk [18].
// dt = [0.0 .. 1.0]
void CalcNewSkeleton(Skeleton start, Skeleton end, float dt)
{
for(int i = 0; i < current_skeleton.bones.Count; i++)
{
// translate
current_skeleton.bones[i].translate = (start.bones[i].translate * (1.0f - dt)) + (end.bones[i].translate * dt);
// rotate
float rotate_x = GetSignedRad(start.bones[i].rotate.X, end.bones[i].rotate.X);
current_skeleton.bones[i].rotate.X = start.bones[i].rotate.X + (rotate_x * dt);
// rotate Y …
// rotate Z …
}
}
// Az "int anim_id"-edik animáció, "float time" másodpercének (pl. 6.5 mp), a pillanatnyi transzformációjának kiszámítása
void SetTime(int anim_id, float time)
{
// aktuális animáció lekérdezése
Animation *anim = animations[anim_id];
// Get Skeleton
int start = (int)Math.Floor(time * anim.fps);
int end = (int)Math.Ceil(time * anim.fps);
if (start == end)
{
CalcNewSkeleton(times[start], times[end], 0.0f);
}
else
{
float skeletonTime1 = (float)start / anim->fps;
float skeletonTime2 = (float)end / anim->fps;
float timeDiff1 = skeletonTime2 - skeletonTime1;
float timeDiff2 = time - skeletonTime1;
float dt = timeDiff2 / timeDiff1;
CalcNewSkeleton(times[start], times[end], dt); // dt = [0.0 .. 1.0]
}
// Update Matrices (transforms)
for(int i = 0; i < currBones.size(); i++)
{
transform[i] = GetMatrix(i);
}
}
· Érdekesség: A régi, Half-Life 1 .SMD fájlban, a háromszög egy csúcsához pontosan egy transzformáció (csont) tartozott. Az új, Half-Life 2 .SMD fájlban a háromszög egy csúcsához 1-3 transzformáció (csont) tartozhat. A csontok súlyozva vannak. A súlyok összege 1,0. Ez az újítás azért van, mert például egy ember könyökénél egy csúcs félig a felkarhoz, félig az alkarhoz tartozik. A súly mondja meg, hogy melyikhez tartozik jobban.
A Half-Life 2-es .SMD fájlban így szerepel egy háromszög [23]:
Kep1.bmp
0 19.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 0.000000 1.000000 1 0 1.0
0 19.250000 -20.500000 -20.500000 0.000000 -1.000000 0.000000 0.000000 0.000000 2 0 0.6 1 0.4
0 60.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 1.000000 1.000000 3 0 0.4 1 0.3 2 0.3
Itt az 1 0 1.0 azt jelenti, hogy egy súlyozott transzformáció tartozik ehhez a csúcshoz. A transzformáció azonosítója a 0, súlya 1.0.
Matrix4 T = Matrix4.Mult(GetMatrix(0), 1.0);
A 2 0 0.6 1 0.4 azt jelenti, hogy két súlyozott transzformáció tartozik ehhez a csúcshoz. Az első transzformáció azonosítója 0, súlya 0.6. A második transzformáció azonosítója 1, súlya 0.4.
Matrix4 T = Matrix4.Mult(GetMatrix(0), 0.6) + Matrix4.Mult(GetMatrix(1), 0.4);
A 3 0 0.4 1 0.3 2 0.3 azt jelenti, hogy három súlyozott transzformáció tartozik ehhez a csúcshoz. Az első transzformáció azonosítója 0, súlya 0.4. A második transzformáció azonosítója 1, súlya 0.3. A harmadik transzformáció azonosítója 2, súlya 0.3.
Matrix4 T = Matrix4.Mult(GetMatrix(0), 0.4) + Matrix4.Mult(GetMatrix(1), 0.3) + Matrix4.Mult(GetMatrix(2), 0.3);
A súlyok összege mindenhol 1.0.
9. Osztály-, Objektum-, és Használati eset diagram:
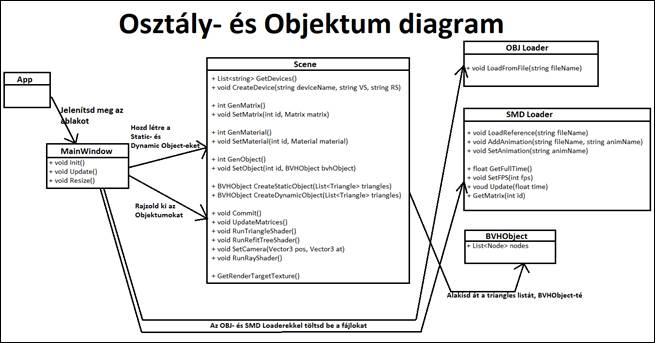
12. ábra: Oszály diagram és Objektum diagram[saját]
Ahogy az objektum diagram mutatja, a „MainWindow” „void Init()” függvénye:
- Létre hozza a „Scene” objektum segítségével az „OpenCL Device” -t.
- Betölti az „OBJLoader” [22] és „SMDLoader” [23] segítségével a „*.obj” és „*.smd” fájlokat.
- A betöltött objektumokat átadja a „Scene” -nek, ami betölti az objektumokat.
A „MainWindow” „void Update()” függvénye:
- Frissíti a mátrixokat a „Scene” objektum segítségével
- Meghívja a TriangleShader-t, RefitTreeShader-t.
- A „void SetCamera(…)” -val beállítja a néző pontot, ami a kezdő sugarakat létre hozza.
- Majd meghívja a RayShader-t, ami kiszámolja a végső színt, amit a sugarak elmetszenek.
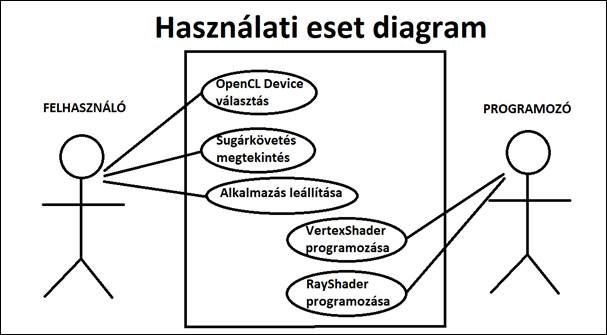
13. ábra: Használati eset diagram[saját]
Két ember használhatja a programot:
- Programozó: Ő írja meg a TriangleShader-t és a RayShader-t.
- Felhasználó: Ő választ „OpenCL device” -t, megtekinti a képet, majd bezárja az alkalmazást.
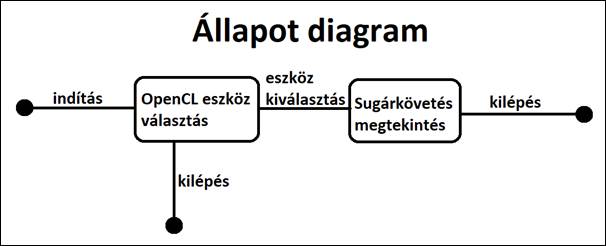
14. ábra: Állapot diagram[saját]
Az alkalmazás állapotai:
- Az alkalmazás indítása után bezárhatjuk, vagy „OpenCL device”-t választahunk.
- Ha device-t választottunk, akkor megtekinthetjük a képet.
-
Majd
bezárhatjuk az alkalmazást.
10. Továbbfejlesztési lehetőségek:
Több továbbfejlesztési lehetőség is van:
Első: A képernyőből induló első metszéspont kiszámítását, nem csak sugárkövetéssel lehet megkapni (ami gépigényes), hanem „OpenGL2.0” vagy „Direct3D9”-el is kiszámíthatók a metszéspontok [19]. Az OpenCL nem rendelkezik „raszterizáló parancsal”, míg az opengl vagy direct3d rendelkezik ilyennel. A raszterizálás azt jelenti, hogy ha van egy háromszögem, aminek ismerem a három csúcs adatait, akkor a videokártya képes kiszámolni a háromszögen belüli pixelek adatait a három csúcsot figyelembe véve. Erre egy külön áramkör áll rendelkezésre a videokártyában. Úgy tudom, ez az áramkör OpenCL-ben, nem elérhető. Ha opengl-t vagy direct3d-t használnék a pixelekből indított sugarak helyett, az akár 100x gyorsabban eredményül adná az első lépésben, a kamerához legközelebbi metszéspontokat. Igaz ilyenkor shader-ben (GLSL, HLSL), kell ügyeskedni.
Második: Ez az OpenCL-es megoldás, amit bemutattam, elavult. Manapság olyan videokártyákat lehet kapni (pl. Nvidia RTX), amik a háromszög-félegyenes metszéspontszámítást elektronikával (chip-el) oldja meg, azaz 1 utasítást kell csak kiadni.
Az én megoldásom, a háromszög-sugár metszéspont számításához, kb. 20-30 utasítást használ (sík-pont távolság, sík-sugár távolság, háromszögen belül van-e a metszéspont), ez lassú.
Harmadik: Ha már sugárkövetés, kihasználhatnám az előnyeit. Indíthatnék sugarakat tükröződési- törési irányba, a diffúz szín kiszámításához [18][19]. Most csak a fényforrásokból indítottam sugarat egy pixel színének kiszámításához.
Negyedik: Az alkalmazás, amikor háromszög-sugár metszéspontot keres, igaz hogy egy objektum egy BVH fa, abban gyors a keresés. De ha sok objektumom van, pl. 100 darab, jelen esetben a program egy „for” ciklussal bejárja mind a pl. 100 objektumot, legközelebbi metszéspontot keresve. Ez nem optimális. Az objektumokat is rendezni kéne a térben. Igaz, ezek az objektumok elmozdulhatnak, ilyenkor „frissíteni” kéne az elrendezést.
Ötödik: A Multi GPU. Vagyis, ha több videokártya van egy számítógépben, akkor ha a képernyőn megjelenő pixelekből induló sugarak egyik felét az egyik vga számolja, míg a képernyőn megjelenő pixelekből indított sugarak másik felét egy másik gpu számolja, akkor majdnem 2x-es sebességel gyorsabb lehet az alkalmazás. A TriangleShader-t egy vga-val kell elvégezni, de a pixelek színének számításához lehetne párhuzamosítani több vga-val. Én ezt nem tettem meg, de elméletileg meg lehet tenni.
Hatodik:
Azt, hogy a sugár a háromszögön belül van-e, azt nem csak vektoriális szorzattal, hanem barycentrikus koordinátákkal is ki lehet számolni.
A háromszög súlya, 1.0. Ha a metszésponttal számolt súlyok összege nagyobb mint 1.0, akkor a háromszögen kívül van a metszéspont.
10.1 BVH fa építése, gyorsan:
Ez megoldás lehet arra, hogy ne "for" ciklussal járjuk be az objektumokat. A gyors BVH fát lehet használni úgy, hogy a fa leveleiben az objektumok vannak, de még gyorsabb megoldás az, ha a háromszögeket tenném a BVH fába. Illetve csak akkor építeném újra a BVH fát, ha animáció van (a háromszögek torzulnak).
Egy megoldást szeretnék mutatni "gyors BVH fa építésére". Ez saját elgondolás, biztosan létezik gyorsabb megoldás erre, ennek ellenére be szeretném mutatni a saját megoldásomat. Most pontokkal fogok dolgozni, ezek a pontok lehetnek az objektumok középpontjai, vagy még jobb, ha a háromszögek lista, egy háromszögének, egyik csúcsa, pl. az "triangle.A" csúcs.
3 lépésből áll a megoldásom:
1. növekvő sorrendbe rendezni valamelyik tengely(X-tengely) szerint a csúcsokat.
2. egy csúcshoz, egy környezeten belül, a legközelebbi szomszédos csúcs megkerése. Így megvannak a levelek, a BVH fa 0. szintje.
3. Alkalmazni a 2. lépést, a további 2., 3. ... N. szintekre addíg, amíg vannak szomszédok. Ha már nincs szomszédja egy befoglaló négyzetnek, az a "root", vagyis a fa gyökere. Így elkészült egy BVH fa.
Most bemutatom a három lépést részletesen:
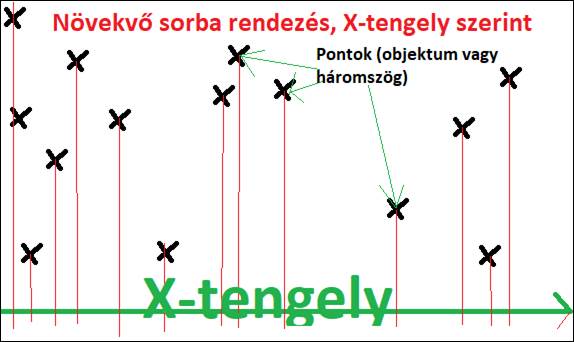
15. ábra: Valamely koordináta-tengely szerindt, rendezni a pontokat (legyen ez pl. az X tengely) [saját]
Ahogy a 15.-es ábra mutatja, rendezzük pl. x tengely szerint növekvő sorrendbe a csúcsokat. Így kapunk egy olyan rendezett csúcs listát, amiben majd ha később keresni szeretnénk, akkor használhatom a "bináris keresést".
Bináris keresés [24]: ha van egy növekvő számsorozat, és meg szeretném tudni hogy szerepel-e benne egy X szám, akkor megtehetem, hogy először a számsorozat közepén lévő Y számmal összehasonlítást végzek. Ha az Y szám nagyobb, mint az X szám, az azt jelenti, hogy a számsorozatnak a második felén, az Y számnál nagyobb számok vannak, ezért azon a részen már nem is kell keresnem, elég csak a számsorozat első felében folytatni a keresést. Egy Y szám összehasonlítással, a sorozat felét el lehet dobni. Majd a sorozaton ismételni ezt az eljárást, addíg felezgetjük a sorozatot, mígy egyszer eljutunk egy számhoz. Ez a szám lesz a legközelebb a keresett X számhoz.
Fontos! Bináris keresést csak rendezett szám sorozaton lehet alkalmazni.
Legelőször a sorba rendezést kell elvégezni. Ezt lehet egy szálon vagy több szálon is végezni. A C# "Array.Sort()" metódusa egy szálon rendezi növekvőbe az elemeket. Ha sok csúcs van, akkor érdemes a sorbarendezést több szálon, több CPU-val végezni.
Már most lehetne BVH fát építeni úgy, hogy a számsorozatban lévő szomszédos számok, egy levelet alkossanak, hiszen x tengely szerint, ők egymáshoz a legközelebb vannak.
Viszont Y és Z tengely is létezik. Mi van akkor, ha két szomszédos pont x tengely szerint pl. 0 méterre vannak egymástól, de ha a pl. az Y vagy Z tengelyt vizsgáljuk, akkor pl. 1km távolságra vannak egymástól a koordináták. Akkor ez az X tengely szerinti szomszédos pont mégsem a legközelebbi? Nem, nem a legközelebbi, mert 1km a távolsága a két pontnak, ha az Y és Z dimenziókat is figyelembe vesszük.
Az én megoldásom az, hogy vegyük a pont jobb oldali környezetét, vizsgáljunk meg nem csak a szomszédos pont távolságát, hanem a szomszéd-szomszédját, illetve annak a szomszédját. Ha sok pontot vizsgálok, nagyobb valószínűséggel találom meg a ponthoz, valószínűleg a legközelebbi pontját.

16. ábra: egy pont környezetét vizsgálva, a szomszédja pont kiválasztása [saját]
Ahogyan a 16. ábra mutatja, vizsgáljuk meg az "A" ponttól, jobbra lévő 6 pontot, és keressük meg a legközelebbi pontot. Így közelítőleg jó szomszédot tudunk találni az "A" ponthoz, és nem kellett az egész számsorozatot bejárni, hogy melyik a biztosan legközelebbi pont. Minél nagyobb környezetet vizsgálunk egy pontnál, annál nagyobb a valószínűség, hogy a legközelebbi pontot találtuk meg. De nekünk most a cél a gyors BVH fa építése, ezért ahogy a kép is mutatja, csak 6 pontot vizsgálok. Ezt ki kell tapasztalni programozáskor, hogy mi a jó határ(6 vagy 20) ahhoz, hogy gyors legyen a fa építése, és annak a bejárása. Ha nagyon nem jó szomszédot találunk egy csúcsnak, nagy lesz a távolság két szomszédos pont között, akkor amikor sugarat indítok, akkor több csomópontra fogja azt mondani a bvh fa, hogy ott lehet háromszög, hiszen nagyobb területű a befoglaló doboz, nagyobb eséllyel mont "igaz" választ egy csomópont arra, hogy van-e sugár-boundingbox metszéspont. Így többet fog számolni az OpenCL, tehát lassabb.
Amikor megtaláltam a számsorozat 0. eleméhez, a szomszédos N pontját, akkor a 0. és N. pontot töröljük a listából, és ez a két ponttal hozzunk létre egy csomópontot. Mivel töröltük a 0. pontot, és az N. pontot a listából, ugyan ezt az eljárást meg lehet ismételni. Megint a 0. indexű ponthoz keressük meg a környezetében lévő szomszédos pontot, és ők is alkossanak egy csomópontot. Ezek a csomópontok kerüljenek bele egy kimeneti listába. Addig ismételjük az eljárást, amíg a bemeneti lista ki nem ürül. Ha egy darab elem marad a bemeneti listában, akkor abból egy olyan csomópontot kell létre hozni, aminek egy levele van.
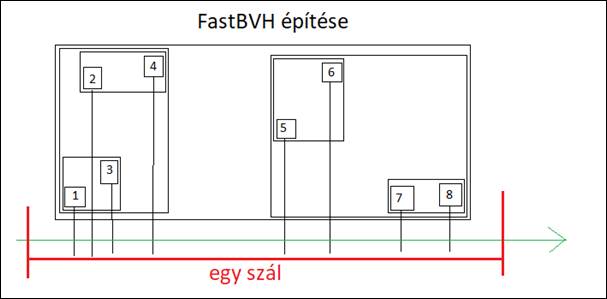
17. ábra: befoglaló négyzetek frissítése, egészen a "root" -ig [saját]
Ahogyan a 17. ábra mutatja, az 1. es csúcs szomszédja a 3. csúcs, pedig X tengely szerint a 2. csúcs közelebb lenne, tehát műlködőképes lehet ez a megoldás.
Majd a kapott kimeneti lista elemeinek számítsuk ki a bounding box-ját, és ismételjük meg a fennti szomszédos keresés eljárást újra, a most már bounding box-okat tartalmazó listában. Mivel a bemeneti listából mindig két elemből, egy elemet készítünk, és azt tesszük a kimeneti listába, így a kimeneti lista minden lépéssel fele akkora lesz, mint a bemeneti lista. Egyszer eljutunk ahhoz az állapothoz, hogy 1 darab bounding box-ot kapunk eredményül. Ő lesz a gyökér "root" elem. A befoglaló négyzetek kiszámítása, amiből nagyon sok van, pont annyi, ahány csomópontja van egy bvh fának, gépigényes. Ha meg van egy szint. pl. a levelek szintje, akkor OpenCL-el a VGA kiszámolhatja párhuzamosan a bounding box-okat, csak az aktuális szint OpenCL Bufferjét kell frissíteni a csomópontokkal.
Így gyorsan BVH fát lehet építeni.
Ez a BVH fa CPU segítségével jött létre. Egy színtér tartalmazhat akár több százezer háromszöget. Ez egy darab szálnak, túl sok idő, míg kiszámolja a BVH fát.
De lehet párhuzamosítani. Ha egy pl. 100.000 pontból álló listát 100 részlistára bontunk, a növekvő sorrendbe helyezés után, akkor a kapott 100 darab részlista, ami darabonként 1000 darab csúcsot ratratlmaz, lehet párhuzamosan, több szálon egyszerre számolni.
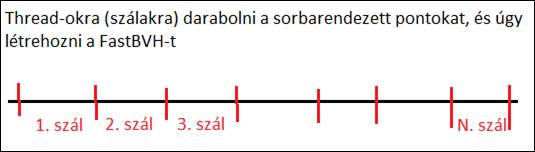
18. ábra: több szálra lehet bontani a szomszédok keresését. [saját]
Ahogyan a 18. ábra is mutatja, az 1. szálban lévő elemek nem használják a 2. szálban lévő elemeket, tehát nincs függőség, lehet párhuzamosítani. Manapság 4-16 magos egy CPU, tehát egyszerre akár 16 szál tud számolni, egymástól függetlenül. Vagyis 16x hamarabb befelyezi egy szál a számítást, mint ha egy szálon számolnánánk csak.
Fotos, először növekvő sorrendbe kell rendezni az egy listát, majd utána lehet darabolni a listatát, több részlistára.
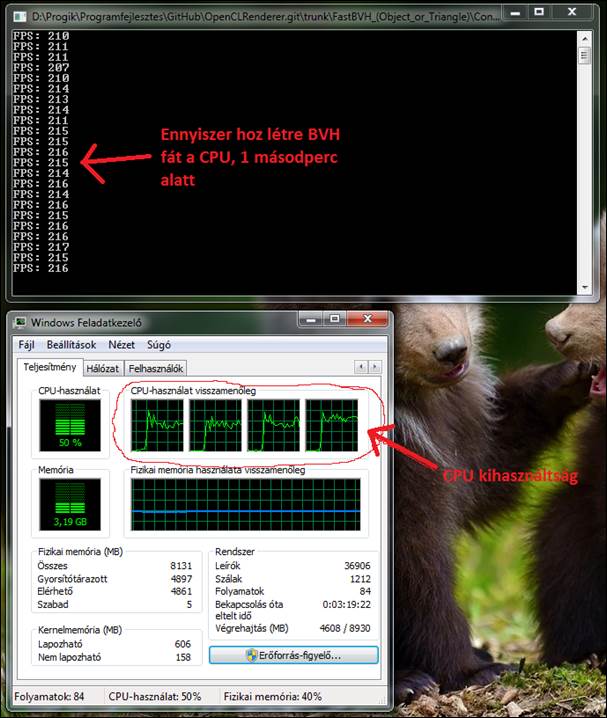
19. ábra: teszt, i5 cpu [saját]
Én ezt a megoldást, amit fennt írtam csak félig programoztam le. A sebességre voltam kíváncsi. Nem számoltam OpenCL-el bounding box-okat. Háromszögekkel végeztem a kísérletet.
35.000 háromszöggel, a sorbarendezés 1 szálon történt a C# "Sort()" függvénnyel, a fa egy szintje 64 szálra/tömbbre lett darabolva. így másodpercenként 200x futott le a a bvh fa építés, egy i5-ös (2. generációs) processzoron, ami 4 magos. Ennek a processzornak a használt piaci ára 10e ft.
Úgy gondolom, hogy ez jó sebesség. Ha azt nézzük, hogy amit megvalósítottam alkalmazást, abban for ciklussal járom be az objektumokat, ezt lehetne helyettesíteni azzal, hogy 1 darab BVH fát építek CPU-val, így benne a keresés jóval gyorsabb, mint ha n. darab BVH fán keresek.
Illetve gyorsítási lehetőség lehet még az, hogy ha megkülömböztetjük a mozdulatlan és az animált háromszögeket. A mozdulatlan háromszögeket tartalmazó BVH fát elég egyszer kiszámolni, míg csak az animált háromszögekre kell csak újra számolni minden frame-ben a BVH fát.
11. Jövőbeli tervek:
Jövőbeli terv lehet az, hogy amit a továbbfejlesztési lehetőségekben leírtam "gyors BVH fa építés"-ét megvalósítom.
Illetve terv lehet még az, hogy jelenleg nem használok a textúráknál "linear interpolation" -t, tehát nagyon pixeles egy textúra, ha közelről mutatja a kamera.
De mivel léteznek professzionális megoldások már, nem biztos hogy tovább foglalkozom ennek a leprogramozásával. Egy év múlva jelenik meg amd oldalon a Playstation 5, ami támogatni fogja a sugárkövetést. Illetve Nvidia oldalon ott van az "RTX", amik léteznek, műlködnek jól.
Az én megoldásomnak előnye lehet, hogy OpenCL és C# létezik sok rendszeren, windows7-en, linux-on, mac os-en, a régi vga-k is támogatják. Nem kell 100e ft-ért RTX-es Nvidia vga-t venni. Igaz, amd oldalon létezik C++ + OpenCL megoldás sugárkövetésre.
12. Felhasználói kézikönyv:
12.1 Letöltés:
Az alkalmazás és forráskód letöltését mutatom be. Először töltsük be ezt a weboldalt: https://github.com/ezszoftver
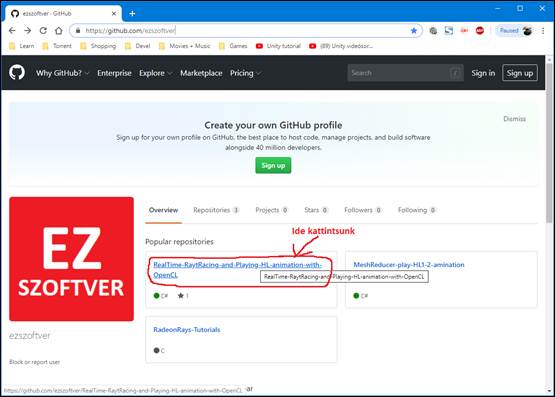
20. ábra: github.com/ezszoftver
Majd kattintsunk a „RealTime-RayTracing” linkre.
Ha a forráskódot akarjuk letölteni, akkor kattintsunk a „download” gombra. Ez a forráskód a pillanatnyi, nem kiadásra szánt forráskód.
Ha a Kiadásra szánt forráskódot és alkalmazást szeretnénk letölteni, akkor kattintsunk a „Releases” linkre.
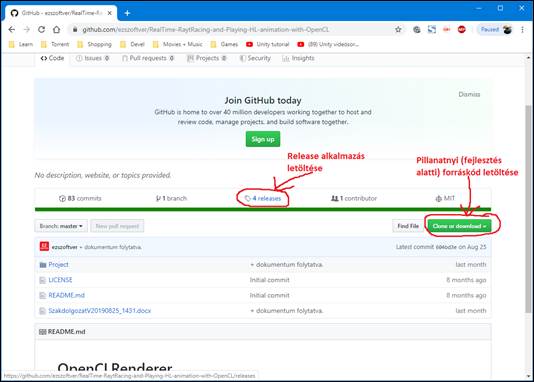
21. ábra: forráskód vagy Release letöltése [saját]
Kattintsunk most a „Releases” linkre.
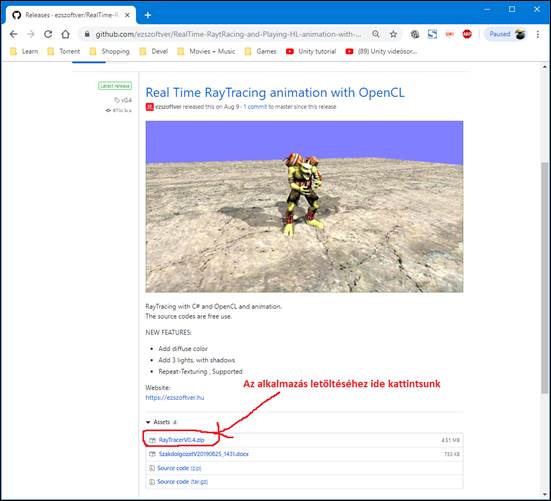
22. ábra: Itt lehet letölteni az alkalmazást [saját]
Majd az alkalmazás letöltéséhez kattintsunk a „RayTracerV0.4.zip” fájlra.
Ezzel letöltöttük az alkalmazást. Itt megtalálható az alkalmazás forráskódja is. Ez nem ugyan az, mint a pillanatnyi fejlesztés alatti forráskód.
12.2 Telepítés:
Csomagoljuk ki a letöltött .zip fájlt.
23. ábra: .zip fájl, kicsomagolva [saját]
12.3 A program használata:
Indítsuk el a kitömörített mappában lévő „Project.exe” fájlt.
24. ábra: Alkalmazás elindítása [saját]
Az alábbi ablak fogad minket:
25. ábra: Válassz OpenCL eszközt [saját]
Az angol szöveg jelentése, „kattints jobb egérgombbal, az OpenCL eszköz kiválasztásához”.
Tegyünk így, válasszunk egy eszközt.
Fontos: Jelenleg OpenCL eszköz, csak GPU (vagyis videokártya) lehet. „CPU”, vagy „Accelerator” OpenCL eszköz nem kerül felsorolásra a helyi menüben.
Ha kiválasztottuk az eszközt, akkor elindul a RealTime Sugárkövetés példaprogram.
Átméretezhető az ablak. Látható a fejlécben, hogy hány új kép készül egy másodperc alatt (FPS). Az alkalmazás bezárásához kattintsunk a jobb felső sarokban található „X” -re.
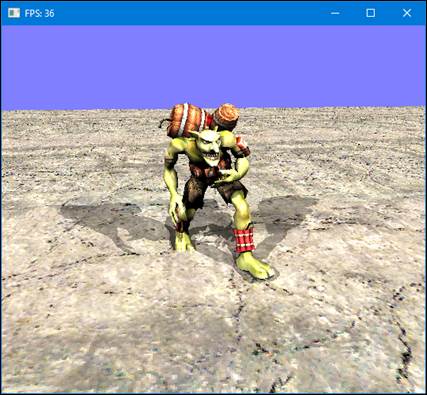
26. ábra: futó alkalmazás [saját]
13. Összefoglalás:
Úgy érzem, hogy sikerült a magamnak felállított célokat elérni. Sikerült egy majdnem használható sugárkövetés alkalmazást megírni, bemutatni. Azért majdnem használható, mert nagyon gépigényes ez az alkalmazás, mert for ciklussal járom be a BVH fákat, ez lassú.
Bemutattam hogyan lehet gyorsan sugár-háromszög metszéspontot számolni, animációt megjeleníteni. Az alkalmazásban, a "RayShader"-ben van példa, hogyan lehet árnyékot számolni sugárkövetéssel.
Illetve célom az is, hogy aki nem ismeri a sugárkövetést, ő most már könnyebben boldoguljon vele, értse az elméletet, hogy hogyan műlködik az én megoldásom.
Segítségemre volt az irodalomjegyzékben lévő leírások, amikből el lehet indulni.
Bemutattam a Vertex shadert, a Ray shadert, és azt, hogy hogyan lehet ezt OpenCL nyelven, ezt megvalósítani.
Sajnos nem platformfüggetlen az alkalmazás, mert WPF ablakot használok a kép megjelenítésére, ami csak windows-on érhető el. De ha a WPF ablakot lecseréljük pl. "Windows Forms" ablakozó rendszerre, akkor a forráskód, linuxon is lefordul a "MonoDevelop" alkalmazással. Tehát ha az ablakozó rendszert leszámítjuk, akkor forráskód szinten, platformfüggetlen az alkalmazás. C# és OpenCL API létezik Linux, Mac rendszerek alatt is.
Bemutattam hogyan lehet .OBJ fájlt betölteni, ami a mozdulatlan modell betöltésekor szóba jöhet, megoldásként.
Illetve bemutattam, hogy hogyan lehet .SMD fájlból csontanimációt betölteni, megjeleníteni. Remélem hogy az animáció megjelenítését érthetően írtam le, úgy, hogy aki nem ismeri ezt, ő ebből a leírásból megértette.
A sugárkövetés téma, régóta létezik, de eddig
(2019), valós időben nem volt elterjedve. Új a téma, ha valós időben akarunk
sugárkövetéssel képet megjeleníteni.
14. Irodalomjegyzék:
1. Szirmai-Kalos László, Csonka György, Csonka Ferenc: Háromdimenzós grafika animáció és játékfejlesztés, Computerbooks, 2005. pp. 486, ISBN: 9636183031.
2. DirectX12 RayTracing tutorials: https://developer.nvidia.com/rtx/raytracing/dxr/DX12-Raytracing-tutorial-Part-1, látogatva: 2020.02.16
3. NVIDIA RTX and DirectX Ry Tracing: https://devblogs.nvidia.com/introduction-nvidia-rtx-directx-ray-tracing/, látogatva: 2020.02.17
4. RadeonRays 2.0 SDK: https://gpuopen.com/gaming-product/radeon-rays/, GitHub: https://github.com/GPUOpen-LibrariesAndSDKs/RadeonRays_SDK, látogatva: 2019.09.27
5. RadeonRays 3.0 SDK: https://www.amd.com/en/technologies/sdk-agreement, látogatva: 2020.02.16
6. NVIDIA Vulkan Raytracing Tutorial: https://developer.nvidia.com/rtx/raytracing/vkray, látogatva: 2020.02.16
7. Vulkan, RayTracing tutorial (C++): https://iorange.github.io/, látogatva: 2020.02.16
8. GPUOpen Libraries: https://github.com/GPUOpen-LibrariesAndSDKs, látogatva: 2020.02.16
9. 3D C++ tutorials: http://www.3dcpptutorials.sk/index.php?id=16, látogatva: 2020.02.16
10. Scratchpixel 2.0: https://www.scratchapixel.com/index.php?redirect, látogatva: 2020.02.17
11. Global Illumination in 99 lines: http://www.kevinbeason.com/smallpt/, látogatva: 202002.17
12. RayTracing in One Weekend: http://in1weekend.blogspot.com/2016/01/ray-tracing-in-one-weekend.html, látogatva: 2020.02.17
13. Daily Pathtracer: http://aras-p.info/blog/2018/03/28/Daily-Pathtracer-Part-0-Intro/, látogatva: 2020.02.17
14. Erdős Zoltán honlapja: https://ezszoftver.hu/, látogatva: 2019.09.27.
15. Erdős Zoltán: EZSzoftver lapja a GitHubon: http://github.com/ezszoftver, látogatva: 2019.09.27
16. Erdős Zoltán: RealTime RayTracing, with Animation alkalmazás forráskódja, https://github.com/ezszoftver/RealTime-RaytRacing-and-Playing-HL-animation-with-OpenCL/releases, látogatva: 2019.09.27
17. Erdős Zoltán: 3D-s animációt lejátszó és objektum-poligonszámot csökkentő alkalmazás forráskódja, https://github.com/ezszoftver/MeshReducer-play-HL1-2-amination/releases, látogatva: 2019.09.27
18. Dr. Szirmay-Kalos László, Antal György, Csonka Ferenc - Háromdimenziós grafika, animáció és játékfejlesztés – ComputerBooks ISBN: 963-618-303-1: https://cg.iit.bme.hu/~szirmay/3Dgraf.pdf
19. Nyisztor Károly – Shaderprogramozás – SZAK Kiadó – ISBN: 978-963-9863-09-5
20. Reiter István – C# programozás lépésről lépésre – Jedlik Oktatási Stúdió Kft. – ISBN: 978-615-5012-17-4
21. IAN MILLINGTON - GAME PHYSICS ENGINE DEVELOPMENT – MK - ISBN-13: 978-0-12-369471-3: http://www.r-5.org/files/books/computers/algo-list/realtime-3d/Ian_Millington-Game_Physics_Engine_Development-EN.pdf
22. .OBJ fájl betöltése, https://en.wikipedia.org/wiki/Wavefront_.obj_file, látogatva: 2020.03.10
23. .SMD fájl betöltése, https://developer.valvesoftware.com/wiki/SDK_Docs, látogatva: 2020.03.10
24. Bináris keresés: Szabó László – Algoritmusok - Eötvös Loránd Tudományegyetem Informatikai Kar: https://www.inf.elte.hu/dstore/document/329/szabo_laszlo_alg2016.pdf
25.
15. Ábrajegyzék:
1. ábra: pont-sík távolsága [saját]
2. ábra: sugár-sík távolsága [saját]
3. ábra: a metszéspont a háromszögen belül van? [saját]
4. ábra: BVH (alterek a gyors kereséshez) [saját]
5. ábra: BVH fák szintjei. Egy szint elemei párhuzamosíthatók OpenCL-el [saját]
6. ábra: textúrakoordináta számítása, a P pontban [saját termék]
7. ábra: Képernyő pixelekből, sugarak előállítása [saját]
8. ábra: sugárkövetés példa (csak tükröződés van benne, törés nincs) [saját]
9. ábra: diffúz színek és árnyékok, RayShader-ben [saját]
10. ábra: árnyék és tükröződés példa [saját]
11. ábra: Scene osztály feladatai [saját]
12. ábra: Oszály diagram és Objektum diagram[saját]
13. ábra: Használati eset diagram[saját]
14. ábra: Állapot diagram[saját]
16. ábra: egy pont környezetét vizsgálva, a szomszédja pont kiválasztása [saját]
17. ábra: befoglaló négyzetek frissítése, egészen a "root" -ig [saját]
18. ábra: több szálra lehet bontani a szomszédok keresését. [saját]
19. ábra: teszt, i5 cpu [saját]
20. ábra: github.com/ezszoftver
21. ábra: forráskód vagy Release letöltése [saját]
22. ábra: Itt lehet letölteni az alkalmazást [saját]
23. ábra: .zip fájl, kicsomagolva [saját]
24. ábra: Alkalmazás elindítása [saját]
25. ábra: Válassz OpenCL eszközt [saját]
26. ábra: futó alkalmazás [saját]
16. Mellékletek:
|
Saját készítésű ingyenes játékaimat és azok forráskódját saját weboldalamon, a https://ezszoftver.hu/-n osztom meg. |
|
|
|
|
|
Saját készítésű forráskódok: csontanimáció, sugárkövetés + dokumentumok a https://github.com/ezszoftver/ -n osztom meg |
|
|
|
|
|
Facebook fórum: https://facebook.com/ezszoftver/ -n érhető el. |
|