3D-s animációt lejátszó
és
objektum-poligonszámot csökkentő alkalmazás
Erdős Zoltán
Budapest
2017.
Tartalomjegyzék
2. A 3D objektumok szerkezetének áttekintése
3. A 3D szoftverekben megvalósított poligonszám-csökkentés áttekintése
5. .OBJ és .SMD fájlok kezelése C# nyelven
5.1. Az .OBJ fájlok fontosabb kulcsszavai
5.3. Animáció kiszámítása és megjelenítése
6. A saját szoftver elkészítése
6.2. A program használatának forgatókönyve
6.3. A számolási hardveregység és a fájlformátumok kiválasztása
6.4. Felület és tesztelés megtervezése
8. Az eredmények összefoglalása, önálló vélemény, javaslattétel
9.3.3. Poligonszám-csökkentett modell mentése
12. Mellékletek: saját készítésű játékaim szájtjai
Dolgozatomban egy megoldást mutatok arra, hogyan lehet betölteni fájlból 3D-s animációt tartalmazó fájlt, majd megjeleníteni OpenGL segítségével, C# nyelven, alkalmazásablakban, illetve hogyan lehet magas felbontású (sok háromszög poligonból álló) modellek poligonszámát viszonylag rövid időn belül csökkenteni.
A projekt C#-os forráskódja letölthető innen: https://github.com/ezszoftver/Zarovizsga [5]. A modelleket, illetve animációt tartalmazó fájl .SMD kiterjesztésű kell legyen.
Manapság a számítógépes játékok nagyon gépigényesek, egy 3D-s modell megjelenítése sok erőforrást használ. Operatív memóriából (RAM-ból) egyre több van a számítógépben, és ezt kihasználva egy-egy modellt több részletezettségben is beletölthetünk. Ekkor kirajzoláskor kiválaszthatjuk, hogy melyik részletezettségűt jelenítjük meg. Így például, ha a modellből sok pixel látszik, mert közel van a kamerához, akkor célszerű azt részletesebben kirajzolni. Míg ha távol van a kamerától, például 100 m-re, akkor csak pár pixel látszik belőle, ezért elegendő valamelyik alacsony részletezettségű verzióját kirajzolni – így gyorsabb lesz a megjelenítése.
A modellek részletezettsége alatt a felületüket borító háromszögpoligonok darabszámát értem. Minél részletezettebb egy modell, annál több háromszögből áll. Animált modelleknél is hasznos a részletezettséget csökkentő program. Dolgozatom a hozzá csatolt forráskóddal egy megoldást mutat a poligonszám-csökkentésre, illetve az animációk betöltésére.
Azért választottam dolgozatom témájának ezt, mert:
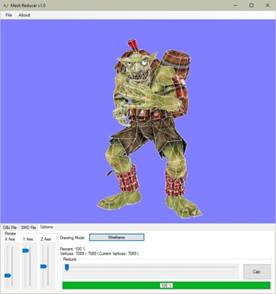
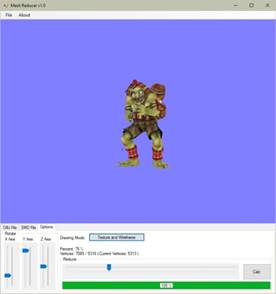
A poligonszám-csökkentő és animáció-megjelenítő algoritmusomat teljesen kidolgoztam. A MeshReducer.exe nevű programban valósítottam meg, amely [5]-ről érhető el. Az 1. ábra a kezelői felületét mutatja a Goblin.smd modellel [11].
A program már a bétatesztelés fázisában van, és csak néhány hiba fordul elő benne.
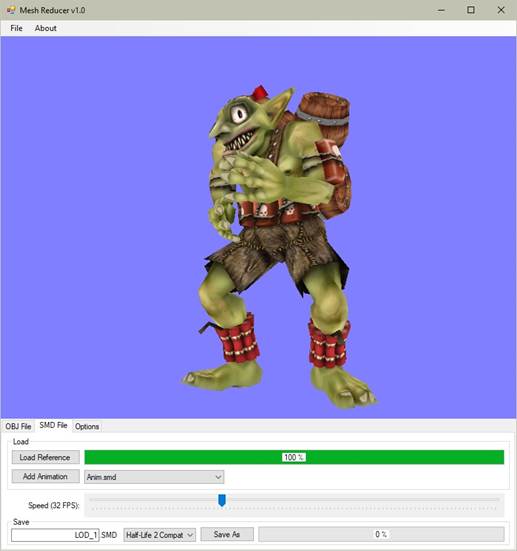
1. ábra: A MeshReducer program felülete [saját termék]
Dolgozatom további fejezeteiben először áttekintést adok a 3D objektumok szerkezetéről, majd a 3D szoftverekben megvalósított poligonszám-csökkentésről. Ezután ismertetem saját algoritmusomat a háromszögpoligonok darabszámának csökkentésére, amelyben módszerem a legrövidebb él megkeresése és törlése. Az algoritmusom szoftveres megvalósításának, a MeshReducer programnak a bemutatása előtt röviden kitérek az .OBJ és az .SMD fájlok kezelésére a projektben általam használt C# nyelven. Az utolsó fő tartalmi fejezetben egy fejlettebb, mások által készített poligonszám-csökkentő algoritmust mutatok be, amely a közel egy irányba néző normálvektorú háromszögek közös élének keresésén alapul. A dolgozat az eredmények összefoglalása után a MeshReducer felhasználói kézikönyvével, majd mellékletben a saját készítésű játékaim szájtjainak bemutatásával zárul.
Vector: Egy x, y, z számhármas. A három szám egy-egy lebegőpontos szám, amelyek együtt egy pontot jelölnek ki a térben.
Háromszög: Három vektorból áll. A, B, C vel jelöljük őket. Fontos a háromszög három vektorjának a sorrendje.
Poligon: Minimum 3 vertexből áll (azaz háromszögpoligon). Ha több vertex van megadva, akkor az alábbi ábra mutatja, hogy hogyan alakul a poligon kinézete.
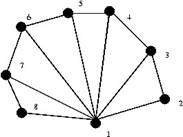
2. ábra: Sok vertexből álló poligon [13]
Textúra illesztés egy háromszögre:
A 1. ábra bal oldalán egy textúra látható. Az OpenGL nem a kép felbontásával dolgozik, hanem [0.0 ... 1.0] lebegőpontos 2D-s koordinátákkal. Amikor kirajzolunk egy A, B, C csúcsot (az ábra jobb oldalán látható), akkor ki kell jelölni a textúrát, majd meg kell adni a 2D textúra koordinátát, és az OpenGL rá illeszti az ábrán látható módon a textúrát a kirajzolandó csúcsokra. Minden egyes A, B, C 3D-s csúcshoz tartozik egy 2D-s textúrakoordináta. Az ábrán jobb oldalon látható az eredmény.
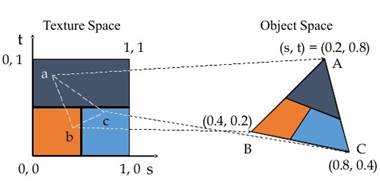
3. ábra: Textúraillesztés egy háromszögre [12]
Térfelosztás: Feldaraboljuk a teret kis kockákra például 2x2x2-es darabszámú kis kockákra. Egy-egy kis kocka háromszögeket tartalmazó listából áll. Majd a zöld színű háromszöget azokba a kiskockákba másoljuk bele, amelyeket elmetsz. Ha meg akarunk keresni a térben egy háromszöget, akkor elég csak abban a kiskockákban keresni, ahol a zöld színű háromszög található.
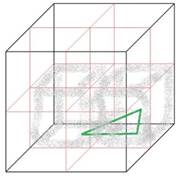
4. ábra: Térfelosztás poligon kereséséhez [14]
Animációt lejátszani és poligonszámot csökkenteni más programokkal (például Blenderrel, 3D Studio Maxszal, Maya-val) is lehet, de azok használata bonyolult, nagy tudást igényel. Ebben a fejezetben a Blenderben található poligonszám-csökkentést mutatom be.
Betöltünk egy objektumot, majd az 5. ábra pirossal mutatott Modifies gombján kattintunk.
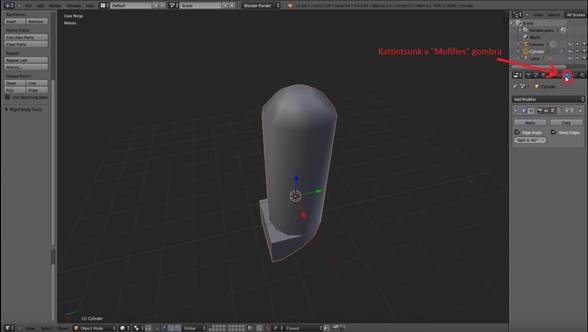
5. ábra: Poligoncsökkentés Blenderben (1/3. lépés): Kattintsunk a Modifies gombra. [saját kép]
Válasszuk ki a Decimate opciót lásd 6 ábra pirossal bekarikázott részén.
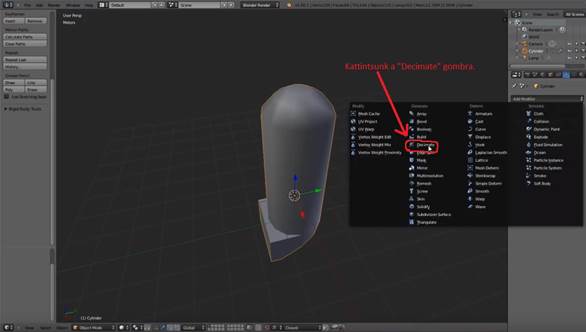
6 ábra: Poligoncsökkentés Blenderben (1/3. lépés): Kattintsunk a Decimate gombra. [saját kép]
A bal egérgombot lenyomva tartva kattintsunk a Ratio gombra (lásd 7. ábra), majd mozgassuk az egeret jobbra-balra.
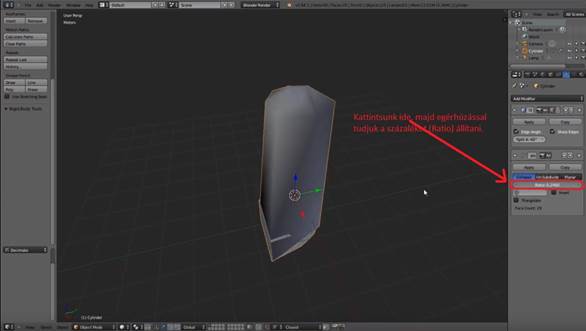
7. ábra: Poligoncsökkentés Blenderben (1/3. lépés): Csökkentés mértékének megadása. [saját kép]
Ebben a fejezetben azt mutatom be, hogyan lehet csökkenteni a modellek háromszögpoligonjainak darabszámát. Az alábbi ábrákon látjuk az algoritmus eredményét a MesReducer program felületén.
8. ábra: Bal oldalon a 100%-os, jobb oldalon 75%-os poligonszámú modell [saját termék]
Először a háromszögpoligonokat alakítsuk ilyen formára:
class Triangle
{
public Vector3 vA, vB, vC;
public Vector2 tA, tB, tC;
public int texture_id,
}
List<Triangle> triangles;
Így háromszögekkel kell dolgoznunk. A List<Triangle> triangles lista eltakarja az .OBJ és az .SMD fájlok felépítését. Most már csak ezzel a triangles listával fogunk foglalkozni. Ezt a listát lehetséges visszaalakítani .OBJ vagy .SMD struktúrára.
A háromszögek darabszámának csökkentésének a lépései, a következők:
1. A legrövidebb él megkeresése a triangles listában.
2. Azoknak a háromszögeknek, amelyek egy csúccsal metszik ezt az élt, a metsző csúcsát az él két csúcsának a számtani közepére kell állítani. A textúra-koordinátákat is hozzá kell igazítani.
3. Töröljük azokat a háromszögeket, amelyek két csúcsukkal is metszik a legrövidebb élt.
4. Ismétlés az 1. ponttól, ha a triangles lista még túl sok háromszöget tartalmaz.
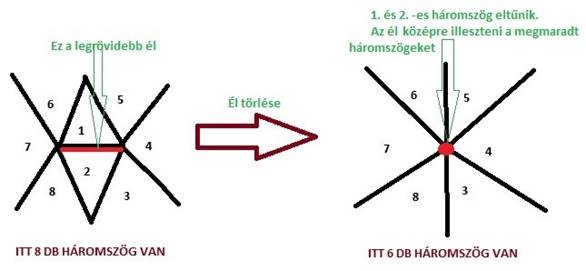
9. ábra: Legrövidebb él törlése [saját ábra]
Most nézzük részletesen a négy lépés algoritmusát.
1. Legrövidebb él megkeresése a triangles listában
„for” ciklussal járjuk végig a háromszögeket, és mérjük meg minden egyes háromszög csúcsai között a távolságokat. Ha találtunk rövidebbet az eddigi legrövidebbtől, akkor tároljuk el azt az élet.
class Edge
{
public Vector3 A;
public Vector3 B;
public int texture_id;
}
Ha több millió háromszögből áll a lista, akkor az él keresése sok időt fog igénybe venni. Tehetjük azt, hogy nem egyesével járjuk be a listát, hanem például véletlenszerűen 1000-szer int id-t generálunk, ami [0 .. (triangles.Count – 1)] értékeket veheti fel, majd csak azokkal a háromszögekkel számolunk. Hozzávetőlegesen jó eredményt ad ez a megoldás is, és sokkal gyorsabb. A véletlen szerű int id a jó megoldás. Ha például 10 000 háromszög van, és minden 10. háromszöget vizsgálnánk mindig, az azért nem lenne jó megoldás, mert akkor nagyrészt mindig ugyanazokat a háromszögeket vizsgálnánk. Például a 3., 7., 9. sohasem lenne vizsgálva. Tehát ezért jobb választás a véletlen szám generálása.
2. Azoknak a háromszögeknek, amelyek egy csúccsal metszik ezt az élt, a metsző csúcsát az él két csúcsának a számtani közepére kell állítani. A textúra-koordinátákat is hozzá kell igazítani.
Ha megvan a legrövidebb él, akkor ki kell számolni az él két csúcsának a közepét: Vector3 P = ((edge.A + edge.B) / 2.0f);, majd meg kell keresni azokat a háromszögeket, amelyek pontosan egy csúccsal metszik el az edge.A-t vagy az edge.B-t. Ezeknek a háromszögeknek az élt metsző csúcsa legyen egyenlő a kiszámolt Vector3 P ponttal.
Majd számoljuk ki az élen lévő két csúcs textúra-koordinátáinak is a számtani közepét. Ez legyen Vector2 tP. Ha az él texture_id-je egyenlő az egy csúccsal metsző háromszög texture_id-jével, akkor a háromszöget metsző csúcsnak a textúra-koordinátáját is le kell cserélni a Vector2 tP-re. Ha nem ugyanaz az él texture_id-je, mint a háromszög texture_id-je, akkor nem csinálunk a háromszög textúra koordinátájával semmit.
3. Töröljük azokat a háromszögeket, amelyek két csúcsukkal is metszik a legrövidebb élt.
Ha a háromszög két metsző csúcsát lecserélnénk az él közepére, akkor a háromszög két ugyan olyan csúcsot tartalmazna, az már nem egy háromszög, hanem egy egyenes lenne. Az nem látszik, törölni kell a listából.
4. Ismétlés az 1. ponttól, ha a „triangles” lista még túl sok háromszöget tartalmaz.
A fenti lépésekkel kevesebb háromszög lesz a listában. Ha még kevesebbet szeretnénk, akkor futtassuk újra az algoritmust az 1. ponttól.
Sebesség optimalizálása
Amikor egy élnek keressük a szomszédos háromszögeit, amelyek tartalmazzák az élt, akkor ezt nem csak a teljes triangles lista bejárásával tehetjük meg. Daraboljuk fel a háromszögeket tartalmazó teret 10x10x10-es kockákra. Minden egyes kocka egy kicsi List<Triangle> triangles lista. Inicializáláskor járjuk be a fő triangles listát, minden egyes háromszögére számoljuk ki az őt metsző kockákat, majd másoljuk a megfelelő kockába a háromszögeket. Így amikor találunk egy élt, elég csak a környezetében lévő kockáknak a háromszögeivel elvégezni a metszésvizsgálatot. Ez akár 10-100-szoros sebességnövekedést is jelenthet.
Egy háromszög több kockába is kerülhet.
Amikor vissza akarjuk állítani a 10x10x10-es kockák kis triangles-eiből a fő (nagy) triangles listát, akkor egy megoldás lehet az, hogy csak azokat a háromszögeket másoljuk a kockákból a fő triangles listába, amelyek még nem szerepelnek a fő (nagy) listában. Ez jó megoldás, de ha a fő triangles lista tartalmaz már például 20 000 háromszöget, akkor sok időbe telik (kb. 0,5 másodpercbe) a listában való keresés, amelynek az ideje folyamatosan növekedne.
Én itt azt a megoldást választottam, hogy mindig csak a lista utolsó 10 000 háromszögével hasonlítok össze. Amelyek régebbi háromszögek a listában, azok valószínűleg távolabbi kockához tartoztak a mostani kockához képest, így kicsi a valószínűsége, hogy ott is elhelyezkedik ugyanaz a háromszög. Így az összehasonlítás ideje jelentősen csökken.
Normálvektorok számítása.
A normálvektorok számításánál is jól jönnek a 10x10x10-es kockák. Egy csúcs normálvektora a csúcsot metsző háromszögek normálvektorainak az átlaga. Amikor keressük a csúcsot metsző háromszögeket, akkor is jól jön az, hogy csak abban a kockában kell keresni a metsző háromszögeket, ahol a csúcs található. A normálvektorokat elég a 10x10x10-es tömb listává alakítása (visszaalakítása) előtt elvégezni. Amikor csökkentjük a háromszögek számát, nincs szükség normálvektorra, nem kell számolni azokat, elég csak a végén.
Ebben a fejezetben egy megoldást mutatok az .OBJ és az .SMD fájlok kezelésére C# nyelven: hogyan lehet megnyitni azokat, hogyan lehet animációt kiszámolni, megjeleníteni. A modell fájlba írását nem mutatom be, mivel ugyanazon az elven működik, mint a beolvasás. A fejezet elkészítéséhez [1] [2] [3] mintakódjait használtam fel.
Az .OBJ fájl viszonylag elterjedt, minden 3D-s szerkesztőben megtalálható. Ez a fájl nem támogatja az animációt. Az .OBJ mellett általában szokott lenni egy .MTL fájl is, amely a textúrákat és az anyagok tulajdonságait írja le.
Az alábbi kulcsszavak szerepelnek egy .OBJ fájlban:
· Megjegyzés:
# ez egy sornyi megjegyzés a fájlban, nem kerül értelmezésre
· Egy csúcspont:
v 2.963193 1.167374 -0.431719
Ha v szöveggel kezdődik egy sor, akkor utána három lebegőpontos szám következik, amelyek egy pontot adnak meg a térben. Ezeket gyűjtsük össze egy List<Vector3> vertices; listába.
· Egy textúra koordináta:
vt 0.875000 0.035000
Ha vt szöveggel kezdődik egy sor, akkor utána két lebegőpontos szám következik, amelyek egy textúra-koordinátát adnak meg. Ezeket gyűjtsük össze egy List<Vector2> textcoords; listába.
· Egy normál vektor:
vn 0.704114 0.480790 0.522556
Ha vn szöveggel kezdődik egy sor, akkor utána három lebegőpontos szám következik, amelyek egy, a felületre merőleges vektort adnak meg. Ezeket is gyűjtsük össze egy List<Vector3> normals; listába.
· Háromszögek:
f 1/2/3 1821/1924/2 609/712/3
Ha f szöveggel kezdődik egy sor, akkor utána szóközökkel elválasztva minimum három vertex következik. Az első vertex 1/2/3 jelentése: Az aktuális csúcs az 1. elem a vertices listából, a csúcshoz tartozó textúra-koordináta a 2. elem a textcoords listából, és a csúcshoz tartozó normálvektor a 3. elem a normals listából. Ne felejtsük el, hogy a lista indexelése 0-tól kezdődik, tehát az 1/2/3 azt jelenti, hogy egy vertex így néz ki:
class Vertex
{
public Vector3 v = vertices[0];
public Vector2 vt = textcoords[1];
public Vector3 n = normals[2];
}
Így van egy vertexünk. Egy háromszöghöz három vertex kell. Ha több vertex szerepel egy sorban, akkor a 4. vertex a 3. és az 1. vertexszel alkot egy háromszöget. Az 5. vertex a 4. és az 1. vertexel alkot egy háromszöget, és így tovább.
· Materiál kijelölése:
usemtl Texture_0
Ha usemtl szöveggel kezdődik egy sor, akkor az utána szereplő materiál-azonosítóval úgymond megmondom, hogy a most következő f-ekre (háromszögekre) ezt a textúrát kell ráhúzni.
· Textúrák és tulajdonságaik:
mtllib cottage.mtl
Ha mtllib szöveggel kezdődik egy sor, akkor utána az .MTL materiálfájl neve szerepel, amely a textúrákat és azok tulajdonságait írja le. Az .MTL fájlban a legfontosabb kulcsszavak az alábbiak:
o newmtl Texture_0: Új materiált hoz létre, amelyre a Texture_0 névvel hivatkozhatunk. Most ez az aktuális materiál.
o mmap_Kd alma.bmp vagy map_Kd alma.bmp: Az aktuális materiál textúrája az alma.bmp. Ez nem mindig szerepel.
o Kd 1.0 0.5 0.0: Az aktuális materiál színe red: 1.0, green: 0.5, blue: 0.0. Ha nincs textúra, akkor a színt kell használni.
· .OBJ fájl kirajzolása:
foreach(Material material in materials)
{
glBindTexture(GL_TEXTURE_2D, material.texture_id);
glBegin(GL_TRIANGLES);
foreach(Vertex vertex in material.vertices)
{
Vector3 v = vertex.v;
Vector2 tc = vertex.tc;
Vector3 n = vertex.n;
glTexCoord2f(tc.X, tc.Y);
glNormal3f(n.X, n.Y, n.Z);
glVertex3f(v.X, v.Y, v.Z),
}
glEnd();
}
Geometriát és animációt tároló .SMD fájlok
Az .SMD kiterjesztésű fájlt a Valve Corporation, 1996-ban alapított, videojátékokat fejlesztő amerikai vállalat hozta létre [9]. A Half-Life 1-2 Half-Life tudományos-fantasztikus belső nézetű lövöldözős (First Person Shooter, FPS) számítógépes játék is ezeket használja ahhoz, hogy animált modelleket jelenítsen meg.
Ez az .SMD kiterjesztésű fájl egy szöveges fájl. Két féle .SMD fájl létezik. Az egyikben mozdulatlan geometriát tárolunk (háromszögek), míg a másik típusban csak az animációt tároljuk. Mind a két féle fájlnak a kiterjesztése .SMD.
Miért kell külön tárolni a geometriát a hozzá tartozó animáció(k)tól? Azért, mert ha mi csak például a „futás” animációt szeretnénk betölteni, akkor elég csak ezt az egy animációt betölteni. Ha egy fájlban lenne a geometria és az összes animáció, akkor olyan animációt is betöltene a program, amelyre nincs szükség. Így tudunk válogatni, hogy mit töltsünk be, és mit ne.
Legelőször a geometriát kell betölteni – ezt kötelező. Utána töltjük be az animáció(ka)t. A geometriát tartalmazó fájlt szokás Reference.smd-nek nevezni, míg az animáció(kat)t tartalmazó fájl(oka)t pedig például Anim.smd-nek. Az .SMD kiterjesztésű fájl létrehozható 3D-s szerkesztőprogramokkal, például MilkShape3D-vel, 3DStudioMaxszal vagy Blenderrel (ehhez be kell kapcsolni a pluginját).
Az alábbi kódban példát látunk a Reference.smd fájl tartalmára:
version 1
nodes
0 "joint1" -1
1 "joint2" 0
2 "joint3" 1
end
skeleton
time 0
0 -0.750000 0.000000 0.500000 1.577046 0.000000 1.570796
1 0.000000 0.000000 40.000790 0.013222 0.000300 3.141593
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
end
triangles
Kep1.bmp
0 19.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 0.000000 1.000000
0 19.250000 -20.500000 -20.500000 0.000000 -1.000000 0.000000 0.000000 0.000000
0 60.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 1.000000 1.000000
Kep1.bmp
0 19.250000 -20.500000 -20.500000 0.000000 -1.000000 0.000000 0.000000 0.000000
0 60.250000 -20.500000 -20.500000 0.000000 -1.000000 0.000000 1.000000 0.000000
0 60.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 1.000000 1.000000
end
Az alábbi kód példa az Anim.smd fájl tartalmára:
version 1nodes0 "joint1" -11 "joint2" 02 "joint3" 1endskeletontime 00 -0.750000 0.000000 0.500000 1.577046 0.000000 1.5707961 0.000000 0.000000 40.000790 0.013222 0.000300 3.1415932 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000time 10 -0.750000 0.000000 0.500000 0.791647 0.000000 1.5707961 -0.000000 -0.000003 40.000549 0.798618 0.000212 -3.1413802 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000time 20 -0.750000 0.000000 0.500000 0.006249 0.000000 1.5707961 -0.000000 -0.000002 39.999920 1.584001 0.000000 -3.1412922 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000end
.SMD fájlok kulcsszavai
Az alábbiakban az .SMD fájlok kulcsszavait mutatom be.
· nodes: Jelentése csomópontok. A csomópontok felsorolása end-ig tart.
nodes
0 "joint1" -1
1 "joint2" 0
2 "joint3" 1
end
Minden sor egy csomópont. Például 1 "joint2" 0 jelentése: ennek a csomópontnak az azonosítója: 1, neve: joint2, a szülejének azonosítója: 0. Célszerű tömbben (listában) tárolni ezeket az adatokat. Ha az i. azonosítójú elemre vagyunk kíváncsiak, akkor a nodes[i] visszaadja az i. azonosítójú csomópont adatait. Ha a szülő azonosítója -1, azt jelenti, hogy ennek a csomópontnak nincs szülője, tehát ez a csomópont a gyökér. Fel lehet rajzolni fagráfban ezeket a csomópontokat, hiszen szülő–gyerek kapcsolat van a csomópontok között.
class Node
{
public:
string name;
public int parent_id;
};
List < Node > nodes;
· bone: Jelentése csont. Egy modell, például az ember mozgatásához csontvázrendszer van létrehozva. Ha mozgatjuk például a törzsünket, akkor vele mozog a hozzá kapcsolt fejünk, karunk. Tehát a csontok között hierarchia van, szülő–gyerek kapcsolat. Sok csont határoz meg egy csontvázat, angolul skeletont. Egy csont lokális transzformációval forogni tud az X, Y, Z tengelyek mentén, és eltolható a szülejéhez képest. Az alábbi kódrészletek egy csontra és egy csontvázra adnak példát.
// egy csont
class Bone
{ // lokális transzformációk. Eltérés a szülőhöz képest
public Vector3 translate;
public Vector3 rotate;
};
// egy csontváz csontok listájából áll
class Skeleton
{
public:
public List < Bone > bones;
};
Illetve egy animáció sok csontvázból áll:
// egy animáció
class Animation
{
public string name; // az aktuális animáció neve (Anim.smd)
public float fps; // 1 sec alatt, hány skeleton játszódik le
public List < Skeleton > times;
};
// sok animáció egy listában
List < Animation > animations;
· time: Jelentése idő.
time 0
0 -0.750000 0.000000 0.500000 1.577046 0.000000 1.570796
1 0.000000 0.000000 40.000790 0.013222 0.000300 3.141593
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
Az animációban vannak a csomópontok (csontok) lokális transzformációi. Például a 0 1.0 2.0 3.0 4.0 5.0 6.0 jelentése: a 0. csomópont lokális mátrixa ez:
Matrix4 local = Matrix4.Translate(1.0, 2.0, 3.0) * Matrix4.RotateXYZ(4.0, 5.0, 6.0);
Vagyis forgatás a tengelyek mentén 4.0, 5.0, 6.0 radiánnal, majd eltolás 1.0, 2.0, 3.0 egységgel. Ha egy modellben például 25 csomópont van, akkor egy time-ban 25 db transzformáció van felsorolva egymás után. Egy time egy pillanatot ábrázol. Ahhoz hogy ebből animáció legyen, ahhoz sok time kell egymás után. 1 másodperc alatt kb. 4-30 time jeleik meg a képernyőn. Két time között kb. 0,2 másodperc telik el. A két time közötti pillanatnyi eltolást lineáris interpolációval, a forgást előjeles szögelfordulással lehet kiszámolni:
times[0].bones[0].translate = new Vector3(1,0,0);
times[0].bones[0].rotate = new Vector(1,0,0);
times[1].bones[0].translate = new Vector(2,0,0);
times[1].bones[0].rotate = new Vector(2,0,0);
Ha például t = 0.2 (t = [0.0 .. 1.0]), akkor a pillanatnyi transzformáció ez:
float t = 0.2;
current_skeleton.bones [0].translate = (times[0].bones[0].translate * (1 - t)) + (times[1].bones[0].translate * t); // lineáris interpoláció
// rotate X
float rotate_x = GetSignedRad(times[0].bones[0].rotate.X, times[1].bones[0].rotate.X);
current_skeleton.bones[0].rotate.X = start.bones[0].rotate.X + (rotate_x * dt);
// rotate Y …
// rotate Z …
Forgásnál fontos, hogy merre forgatunk. Például ha a kezdő szög 0,1 radián, a vég szög pedig 6,27 radián, akkor -0,2 radiánnal kell forogni az óra járásával megegyező irányba. Itt nem lehet lineáris interpolációval számolni, mert 6,26 radiánnal forogna az óra járásával ellentétes irányba.
· skeleton: Jelentése csontváz. time-ok vannak benne end végjelig:
skeleton
time 0
0 -0.750000 0.000000 0.500000 1.577046 0.000000 1.570796
1 0.000000 0.000000 40.000790 0.013222 0.000300 3.141593
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
time 1
0 -0.750000 0.000000 0.500000 0.791647 0.000000 1.570796
1 -0.000000 -0.000003 40.000549 0.798618 0.000212 -3.141380
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
time 2
0 -0.750000 0.000000 0.500000 0.006249 0.000000 1.570796
1 -0.000000 -0.000002 39.999920 1.584001 0.000000 -3.141292
2 0.000000 0.000000 59.751438 0.000000 -0.000000 0.000000
end
Például egy time 0 leírja a 0. időben a csomópontok transzformációit, vagyis az aktuális csontváz csontjainak helyét és forgási szögeit. A Reference.smd fájlban csak egy time szerepel, ez a kezdeti beállása a modellnek. Míg az Anim.smd fájlban sok time szerepel, mindegyik leírja hogy az i. time-ban mi az aktuális csontváz, vagyis az aktuális transzformációk.
Egy csomópontnak úgy tudjuk kiszámolni a globális koordináta-rendszerben a transzformációját a lokális transzformációból, hogy vesszük a lokális transzformációt, majd rekurzívan összeszorozzuk a szülejének a lokális transzformációjával, azután a szülő szülejének a lokális transzformációjával addig, amíg el nem jutunk a gyökérig. A gyökér csomópont transzformációja az egység mátrix.
Itt egy példakód erre:
Matrix4 GetMatrix(int bone_id)
{
if (bone_id == -1) return Matrix4.Identity; // egységmátrix, ha a gyökérben vagyunk
// lokális transzformáció. Eltérés a szülőhöz képest
Vector3 r = currBones[bone_id].rotate;
Vector3 t = currBones[bone_id].translate;
Matrix4 local = Matrix4.Translate(t.X, t.Y, t.Z) * Matrix4.RotateXYZ(r.X, r.Y, r.Z);
// szülő transzformáció kiszámítása, rekurzívan
Matrix4 parent = GetMatrix(nodes[bone_id].parent_id);
// visszatérünk az aktuális transzformációval
return Matrix4.Mult(parent, local);
}
· triangles: A triangle jelentése háromszög poligon. Háromszögek felsorolva end végjelig. Egy háromszög így néz ki:
texture.bmp
1 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
2 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
3 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
Ez azt jelenti, hogy erre a háromszögre a texture.bmp-t kell illeszteni. Utána szerepel három sor. Minden sor egy csúcsot ír le. Az első sor ez: 1 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0. Ez azt jelenti, hogy a háromszög egyik csúcsa [1.0, 2.0, 3.0], normálvektora [4.0, 5.0, 6.0], textúra-koordinátája [7.0, 8.0]. Az első szám az 1-es azt jelenti, hogy ehhez a csúcshoz az első indexű csomópont tartozik. Így már hozzá van rendelve egy csúcs egy transzformációhoz.
Amikor animációt akarunk megjeleníteni, elég csak kiszámítani a pillanatnyi transzformációkat, majd a megfelelő csúcsokra alkalmazni.
Végigjárjuk a materials listát, kijelöljük az aktuális textúrát, majd a material minden egyes csúcspontját transzformáljuk, majd kirajzoljuk OpenGL segítségével:
void Draw()
{
glPushMatrix();
for(int i = 0; i < materials.Count; i++)
{
Material mat = materials[i];
glBindTexture(gl.GL_TEXTURE_2D, mat.texture_id);
glBegin(GL_TRIANGLES);
for(int j = 0; j < mat.vertices.Count; j++)
{
Vertex in = mat.vertices[j];
Matrix4 T = transform[in.id] * transformInverse[in.id]; // transzformáció kiszámítása
Vector3 v = T * Vector4(in.position, 1);
Vector3 n = T * Vector4(in.normal , 0); // itt nincs eltolás, csak forgás van
Vector3 t = in.texCoord;
glTexCoord2f(t.X, t.Y);
glNormal3f(n.X, n.Y, n.zZ);
glVertex3f(v.X, v.Y, v.Z);
}
glEnd();
}
glPopMatrix();
}
Mit is jelent a kirajzolásnál az alábbi sor?
Matrix4 T = transform[in.id] * transformInverse[in.id]; // transzformáció kiszámítása
Ez azt jelenti, hogy két listánk van. Egy List < Matrix4 > transform; és egy List < Matrix4 > transformInverse;.
A transform lista a pillanatnyi csontváz transzformációit tartalmazza. Ezt minden képkockán (frame-en) ki kell számítani:
for(int i = 0; i < currBones.size(); i++)
{
transform[i] = GetMatrix(i);
}
A transformInverse lista pedig a Reference.smd fájlban található egyetlen csontváz transzformációinak inverzét tartalmazza. Ez mit is jelent? A Reference.smd fájlban található egyetlen csontváz adott, és a csúcspontok is adottak. Nevezzük el a Reference.smd fájlban található csontváz i. transzformációját T-nek, és a Reference.smd fájlban található egyik háromszög egyik csúcsát out-nak. Ha elképzeljük, akkor: Vector3 out = T * ?; Tehát adott az out vektor és a T mátrix a Reference.smd fájlban. A ? az ismeretlen, amire szükségünk lesz, ezért ki kell számítani.
Amikor a pillanatnyi animációt akarom megjeleníteni, akkor azt így kell: Vector3 v = transform[i] * ?;
Tehát fejezzük ki a ?-et: Vector3 out = T * ?; // átalakítás (fejezzük ki a ?-et)
1. egyenlet: Vector3 ? = Matrix4.Inverse(T) * out;
Ha megvan a ?, akkor:
2. egyenlet: Vector3 v = transform[i] * ?;
Egybe a két egyenlet: Vector3 v = transform[i] * inverse(T) * out; Így Vector3 v az aktuális animáció egyik csúcspontja.
Ezért szerepel a Draw() metódusban a fenti megoldás.
A transformInverse listát elég egyszer kiszámítani, például a Reference.smd fájl betöltése után:
Matrix4 GetRefMatrix(int bone_id)
{
if (bone_id == -1) return Matrix4.Identity; // egységmátrix, ha a gyökérben vagyunk
// lokális transzformáció. Eltérés a szülőhöz képest
Vector3 r = referenceSkeleton.bones[boneId].rotate;
Vector3 t = referenceSkeleton.bones[boneId].translate;
Matrix4 local = Matrix4.Translate(t.X, t.Y, t.Z) * Matrix4.RotateXYZ(r.X, r.Y, r.Z);
// szülő transzformáció kiszámítása, rekurzívan
Matrix4 parent = GetRefMatrix(nodes[bone_id].parent_id);
// visszatérünk az aktuális transzformációval
return Matrix4.Mult(parent, local);
}
for(int i = 0; i < referenceSkeleton.bones.Count; i++)
{
transformInverse[i] = Matrix4.Inverse(GetRefMatrix(i));
}
A SetTime(float time) metódusban pedig a pillanatnyi csontvázat kell kiszámolni, amelyet majd később kirajzolunk.
// dt = [0.0 .. 1.0]
void CalcNewSkeleton(Skeleton start, Skeleton end, float dt)
{
for(int i = 0; i < current_skeleton.bones.Count; i++)
{
// translate
current_skeleton.bones[i].translate = (start.bones[i].translate * (1.0f - dt)) + (end.bones[i].translate * dt);
// rotate
float rotate_x = GetSignedRad(start.bones[i].rotate.X, end.bones[i].rotate.X);
current_skeleton.bones[i].rotate.X = start.bones[i].rotate.X + (rotate_x * dt);
// rotate Y …
// rotate Z …
}
}
// Az "int anim_id"-edik animáció, "float time" másodpercének (pl. 6.5 mp), a pillanatnyi transzformációjának kiszámítása
void SetTime(int anim_id, float time)
{
// aktuális animáció lekérdezése
Animation *anim = animations[anim_id];
// Get Skeleton
int start = (int)Math.Floor(time * anim.fps);
int end = (int)Math.Ceil(time * anim.fps);
if (start == end)
{
CalcNewSkeleton(times[start], times[end], 0.0f);
}
else
{
float skeletonTime1 = (float)start / anim->fps;
float skeletonTime2 = (float)end / anim->fps;
float timeDiff1 = skeletonTime2 - skeletonTime1;
float timeDiff2 = time - skeletonTime1;
float dt = timeDiff2 / timeDiff1;
CalcNewSkeleton(times[start], times[end], dt); // dt = [0.0 .. 1.0]
}
// Update Matrices (transforms)
for(int i = 0; i < currBones.size(); i++)
{
transform[i] = GetMatrix(i);
}
}
· Érdekesség: A régi, Half-Life 1 .SMD fájlban, a háromszög egy csúcsához pontosan egy transzformáció (csont) tartozott. Az új, Half-Life 2 .SMD fájlban a háromszög egy csúcsához 1-3 transzformáció (csont) tartozhat. A csontok súlyozva vannak. A súlyok összege 1,0. Ez az újítás azért van, mert például egy ember könyökénél egy csúcs félig a felkarhoz, félig az alkarhoz tartozik. A súly mondja meg, hogy melyikhez tartozik jobban.
A Half-Life 2-es .SMD fájlban így szerepel egy háromszög:
Kep1.bmp
0 19.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 0.000000 1.000000 1 0 1.0
0 19.250000 -20.500000 -20.500000 0.000000 -1.000000 0.000000 0.000000 0.000000 2 0 0.6 1 0.4
0 60.250000 -20.500000 20.500000 0.000000 -1.000000 0.000000 1.000000 1.000000 3 0 0.4 1 0.3 2 0.3
Itt az 1 0 1.0 azt jelenti, hogy egy súlyozott transzformáció tartozik ehhez a csúcshoz. A transzformáció azonosítója a 0, súlya 1.0.
Matrix4 T = Matrix4.Mult(GetMatrix(0), 1.0);
A 2 0 0.6 1 0.4 azt jelenti, hogy két súlyozott transzformáció tartozik ehhez a csúcshoz. Az első transzformáció azonosítója 0, súlya 0.6. A második transzformáció azonosítója 1, súlya 0.4.
Matrix4 T = Matrix4.Mult(GetMatrix(0), 0.6) + Matrix4.Mult(GetMatrix(1), 0.4);
A 3 0 0.4 1 0.3 2 0.3 azt jelenti, hogy három súlyozott transzformáció tartozik ehhez a csúcshoz. Az első transzformáció azonosítója 0, súlya 0.4. A második transzformáció azonosítója 1, súlya 0.3. A harmadik transzformáció azonosítója 2, súlya 0.3.
Matrix4 T = Matrix4.Mult(GetMatrix(0), 0.4) + Matrix4.Mult(GetMatrix(1), 0.3) + Matrix4.Mult(GetMatrix(2), 0.3);
A súlyok összege mindenhol 1.0.
Amikor kirajzolunk egy modellt a képernyőre, jó lenne, ha minél rövidebb lenne a kirajzolás ideje. Így gyengébb teljesítményű gépeken is futna a játék, szélesebb lenne a célközönség, többen használhatnák, vásárolnák meg a programot.
Animációt lejátszani és poligonszámot csökkenteni más programokkal (például Blenderrel, 3D Studio Maxszal, Maya-val) is lehet, de azok használata bonyolult, nagy tudást igényel.
A program először betölt egy .OBJ (nem animált modellt tartalmazó) fájlt vagy .SMD (animált modellt tartalmazó) fájlt. Megjeleníti a modellt vagy lejátsza az animációt. Majd csúszka segítségével a felhasználó kiválaszthatja százalékban a kívánt a részletezettségi szintet. Például, ha 10%-ot választ, az azt jelenti, hogy az eredeti modell háromszögeinek száma (100%) az új modellben az 1/10-e lesz (10%). A program elvégzi a kívánt számításokat, majd a felhasználó kimentheti a csökkentett poligonszámú modellt .OBJ vagy .SMD formátumba.
Az én megoldásom a CPU segítségével számolja az animációt és a háromszögek csökkentését. A program egy szálon fut.
Az animáció megjelenítését (mátrix-vektor szorzás) a videokártya is végezhetné. A videokártyát épp azért hozták létre, hogy az ilyen számításokat elvégezze a CPU helyett, tehermentesítse azt.
A poligonszám-csökkentésnél a legrövidebb él megkeresését, párhuzamos számítással is lehetne megoldani. Az egyik megoldás, ha több szálon számolna a CPU. Lehetne OpenCL segítségével is számolni, így a CPU vagy GPU is végezhetné a számolást.
Én azért maradtam a CPU-nál, mert így egyszerűbb elkészíteni a programot. Animáció megjelenítésénél csak egy modellt kell megjeleníteni, aminek számításait a mai CPU-k elbírják végezni. Ha több, 10-1000 modellt kellene megjeleníteni, akkor az animációt GPU-val számolnám ki.
Mivel a poligonszám-csökkentés feladatban csak egy kis részen lehet párhuzamosítani, a legrövidebb él keresésénél, úgy gondoltam, nem éri meg bonyolultabbá tenni a programot a többszálúsítással. Csak kb. fél perc lenne a nyereségünk.
Azért választottam az .OBJ és .SMD fájlformátumokat, mert ezeket a legkönnyebb megérteni, feldolgozni. Ezek a kiterjesztésű fájlok nem bináris, hanem szöveges fájlok, könnyebb az értelmezésük, illetve általánosan elterjedtek, használtak a számítógépes grafikában.
A felületet egyszerűre akartam megtervezni, füles szerkezetűre (lásd 10. ábra. Szükség van OBJ File fülre, ahol az .OBJ fájlok kezelése történik: betöltésük és kimentésük. Valamint szükség van SMD File fülre az .SMD fájlokhoz: betöltésük és kimentésük. A modellek kezeléséhez külön fülre kerültek a funkciók, neve Options lett. Itt lehet forgatni a modellt, csúszka segítségével csökkenteni a részletezettségét, illetve a kirajzolás típusát lehet beállítani. Más grafikai elemre nincs szükség.
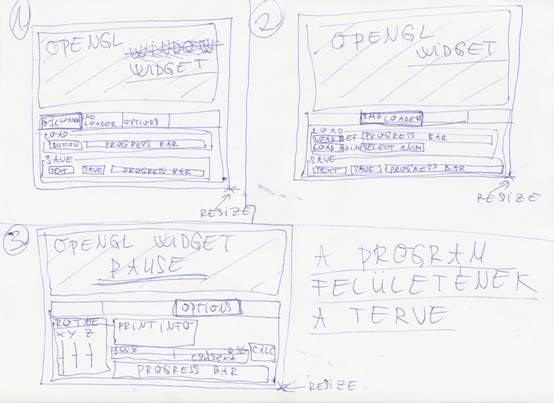
10. ábra: A MeshReducer program felületének terve [saját termék]
Programozás közben debuggolással teszteltem a programot. Illetve, amikor elkészült az alkalmazás, fontossá vált, hogy a kivételeket jól leteszteljem, és mindet megfelelően kezeljem. „Ne szálljon el a program”, ha a felhasználó például nem megfelelő fájltípust választ ki. Viszont ha pl. .ZIP fájlt átnevez .OBJ kiterjesztésűre, majd azt akarja betölteni, akkor baj van. (Az .OBJ fájlnak nincs speciális fejléce, nem lehet azonosítani, hogy ő egy .OBJ fájl).
A programban kiszámolt normálvektorok megfelelőségét úgy ellenőriztem, hogy az exportált modellt megnyitottam Blenderben (lásd 11. ábra).
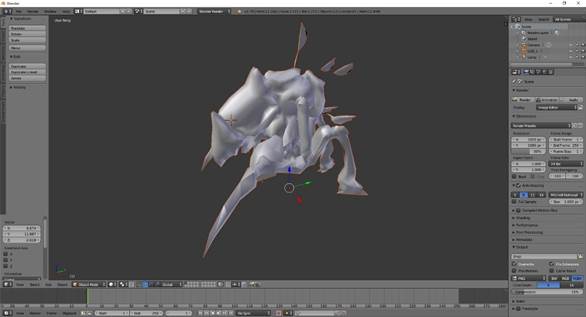
11. ábra: Kiszámolt normálvektorok megfelelőségének tesztelése: exportált fáj megnyitása Blenderben [saját ábra]
A programkészítés során megvalósítandó legfontosabb funkciók az alábbiak:
1. .OBJ vagy .SMD fájl betöltése, amelyek tartalmából Mesh objektum lesz. A Mesh objektummal lehet textúrákat betölteni.
2. Ha a MainWindow ablakban a Reduce gombra kattintva az aktuális Mesh objektumból MeshReducer készítése, és poligonszámának csökkentése
3. A lecsökkentett poligonszámú modell visszaalakítás Mesh objektumra. Ezt ki lehet rajzolni, és ki lehet menteni .OBJ vagy .SMD fájlba.
A 12. ábra a MeshReducer program objektumai közötti kapcsolatokat mutatja.
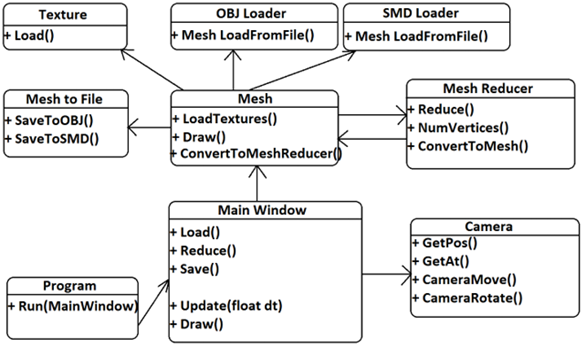
12. ábra: A MeshReducer program objektumai közötti kapcsolat diagramja [saját ábra]
Létezik olyan megoldás is, ahol nem a legrövidebb élt kell megkeresni és törölni, hanem azt az élt, amely arra a két háromszögre illeszkedik, amelyek normálvektorai közel egy irányba néznek.
Ilyenkor, ha két szomszédos háromszög úgymond egy síkban van, akkor erről a síkról lehet törölni háromszögeket, hiszen úgysem vesszük észre, ha egy nagy síkot például nem 5, hanem 2 darab háromszög alkot.
Ez a gondolatmenet egy továbbfejlesztése az én megoldásomnak.

13. ábra: Példamodell a közel egy irányba néző normálvektorú háromszögek közös élének keresésével végzett poligonszám-csökkentésre [10]
A MeshReducer programmal most már tudunk
· .OBJ és .SMD fájlt betölteni,
· .SMD fájlból animációt lejátszani,
· modell poligonszámát csökkenteni,
· exportálni a modellt .OBJ vagy .SMD fájlba.
Véleményem szerint az animációt megjelenítő algoritmust lehetne árnyalóval (shaderrel) is számolni, úgy gyorsabb lenne a megjelenítés. Most egy csúcs kirajzolása egy OpenGL függvény hívás. Ha 10 000 darab csúcsunk van, az 10 000 darab függvényhívás.
Viszont a CPU-s megoldás az érthetőbb, egyszerűbb. CPU-val könnyebb elvégezni egy matrix-vektor szorzást, majd kirajzolni vertexenként egyesével a modellt, mint vertexet tartalmazó tömböt létrehozni, transzformációkat tartalmazó tömböt létrehozni, átadni a VGA-nak, majd shaderben megírni a mátrix-vektor szorzást.
Lehetne megvilágítást is számolni, az bizonyítaná, hogy a program által kiszámolt normálvektorok valóban jók. De ha megnyitom az exportált fájlokat például Blenderben, akkor a megvilágítás rendben van, tehát jók a normálvektorok.
Ez a fejezet a MeshReducer program felhasználói kézikönyvét tartalmazza.
A program és a hozzá tartozó forráskód ingyenes.
Az alkalmazást innen lehet letölteni: https://github.com/ezszoftver/Zarovizsga.
Telepíteni nem kell, de a program futtatásához szükséges minimum
· Windows 7 64 bites operációs rendszer,
· .NET 4.6,
· Visual Studio 2015 Redistributable x64,
· Opengl 2.0 videokártya.
Ha a videokártya DirectX9-es, akkor ismeri az OpenGL2.0-t is. Fennt kell lennie a VGA driverjének.
A programot elindítani a MeshReducer\MeshReducer\bin\x64\Release\MeshReducer.exe-vel lehet.
|
Ha elindítjuk a MeshReducer.exe-t, akkor először az 14. ábra által mutatott ablak fogad minket. Itt a felső nagy, kék részen fog megjelenni a modell. Alatta füleket találunk. Ha .OBJ fájlt akarunk betölteni, az OBJ File fülön kattintsunk a Load gombra. |
14. ábra: A MeshReducer program képernyője induláskor [saját termék] |
Ha kitallóztunk egy fájlt, például a Zarovizsga\OBJ\OBJ_export\cottage.obj .OBJ fájlt, akkor ez a kép fogad minket (a házikó letölthető innen: http://www.3DRT.com).
Jobb alul folyamatjelző sáv (ProgressBar) mutatja a modell betöltésének állását. A 15. ábra modelljének betöltöttsége már 100%.
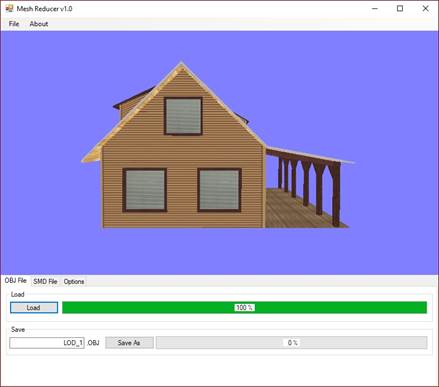
15. ábra: A cottage.obj mejelenése a MeshReducer programban [saját termék]
A kamerát a billentyűzet nyilaival és az egér mozgatásával lehet mozgatni (az egér jobb gombja legyen lenyomva mozgatás közben). Így lehet körbejárni a modellt.
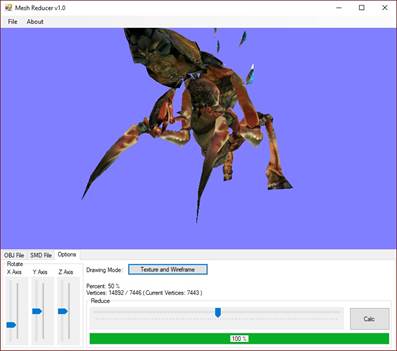
A modellt az X, Y és Z tengelyek mentén az Options fülre (lásd 16. ábra) átkattintva tudjuk forgatni.
Az Options fülön rajzolási stílust is választható:
Az Options fülön a Reduce csúszkájával válasszuk ki a nekünk megfelelő részletezettségi szintet. A poligonszámcsökkentés elindításához kattintsunk az ablak jobb alsó sarkában elhelyezkedő Calc gombra. Ekkor alul egy folyamatjelző sáv (ProgressBar) elkezd 0%-ról, 100%-ra menni. Ha a konvertálás elérte a 100%-ot, a képernyőn megjelenik a kiválasztott részletezettségű modell.
A program a Reduce csúszka felett nem csak százalékban, hanem vertexszámban is kiírja, hogy hány csúcsból áll a modell.
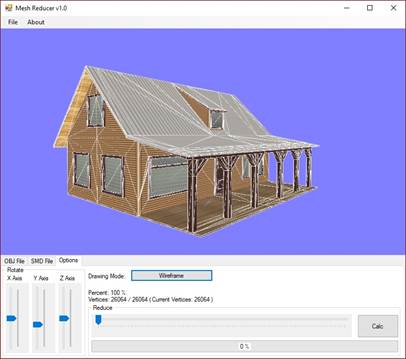
16. ábra: A MeshReducer Options füle [saját termék]
Ha .SMD modellt akarunk betölteni, akkor válasszuk az SMD File fület, majd ott kattintsunk a Load Reference gombra. Fontos hogy itt a geometriát tartalmazó .SMD fájlt tallózzuk ki.
Ez például a Zarovizsga\SMD\HL2\Antlion\Antlion_guard_reference.smd fájl (ez a modell egy Half-Life 2-ből kiszedett modell) Ekkor ismét elindul a folyamatjelző sáv, és ha felért 100%-ra, megjelenik a mozdulatlan modell (lásd 17. ábra).
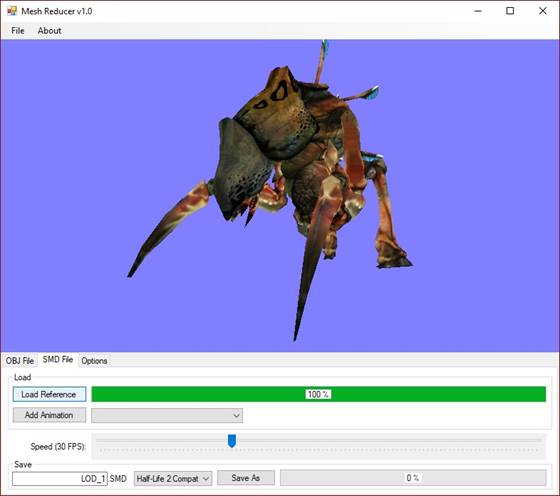
17. ábra: A betöltött Antlion_guard_reference.smd a MeshReducer ablakban [saját termék]
Majd az Add Animation gombra kattintva töltsünk be egy animációt. Fontos, hogy itt azt az .SMD fájlt válasszuk ki, amely nem a geometriát, hanem a sok csontvázat tartalmazza. Ez például a Zarovizsga\SMD\HL2\Antlion\idle.smd lehet.
Majd válasszuk ki a kombinált listában (ComboBoxban) az animációt, például az idle.smd fájlt (lásd 18. ábra), és az automatikusan elindul.
Az animáció sebességet a Speed csúszkával lehet változtatni.
Fontos, hogy a geometria .SMD fájl, és a hozzá tartozó animáció .SMD fájl összetartozik. Ne tallózzunk ki más geometriához tartozó .SMD animáció fájlt.
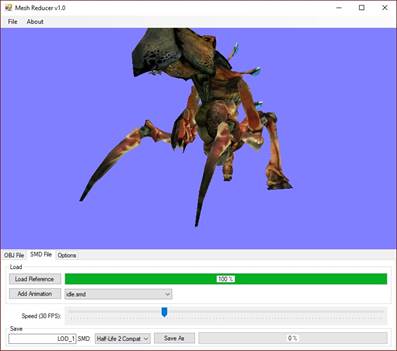
18. ábra: Az idle.smd kiválasztása a MeshReducer felületén [saját termék]
A kameramozgás ugyan az, mint ha .OBJ fájlt töltöttünk volna be.
A Reduce csúszka is ugyanúgy működik, mint az .OBJ leírásánál.
A 19. ábra azt mutatja, hogy hogyan néz ki az animáció, ha 50% a részletezettség az eredetihez képest.
19. ábra: Animáció az 50%-os részletezettségű Antlion guarddal [saját termék]
Ha kiválasztottuk a megfelelő részletezettséget, akkor a modellt kimenthetjük .SMD vagy .OBJ fájlba.
Először nézzük az .SMD mentését:
Ha folyamatjelző sáv felmegy 100%-ra, sikeres volt a mentés. A fájlt abba a mappába hozza létre a program, ahol a geometriát tartalmazó .SMD fájl található.
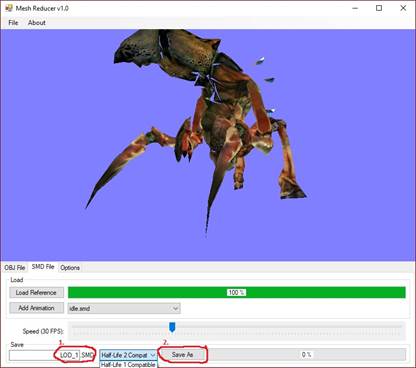
20. ábra: Ploligonszám csökkentett SMD fájl mentése [saját termék]
Ha .OBJ formátumba akarjuk kimenteni az aktuális részletezettségű modellt, akkor:
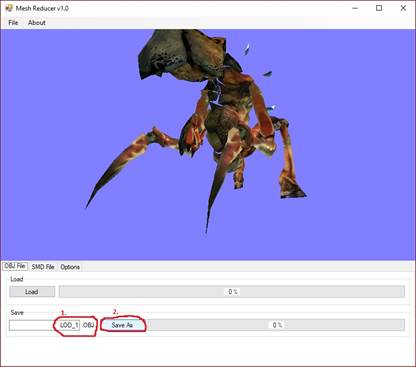
21. ábra: Poligonszám csökkentett OBJ fájl bentése [saját termék]
Ha a menüsoron (MenuBar) az About menüpontra kattintunk, előjön egy kis leírás, hogy Mikor, ki készítette a programot. OK-val zárhatjuk be az About ablakot.
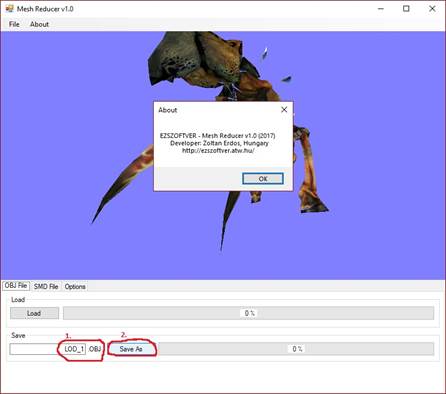
22. ábra: A MeshReducer About ablaka [saját termék]
A programból kilépni a jobb felső sarokban található X gombbal lehet vagy a menüsoron a File/Exit menüpontra kattintva.
1. Szirmai-Kalos László, Csonka György, Csonka Ferenc: Háromdimenzós grafika animáció és játékfejlesztés, Computerbooks, 2005. pp. 486, ISBN: 9636183031.
2. Nyisztor Károly: Grafika és játékprogramozás DirectX -szel, SZAK kiadó, 2005
3. Nyisztor Károly: Shaderprogramozás (Grafika és játékfejlesztés DirectX -szel), SZAK kiadó, 2009
4. OpenGL 1.5, in 3D C/C++ tutorials, http://www.3dcpptutorials.sk/index.php?id=14, 2017.10.28
5. Erdős Zoltán honlapja, utolsó módosítás: 2016.06.06., http://ezszoftver.atw.hu/, látogatva: 2017.10.28.
6. Erdős Zoltán: EZ Szoftver lapja a GitHubon: http://github.com/ezszoftver, látogatva: 2017.10.28
7. Christopher G. Healey: 3D Modeling and Parallel Mesh Simplification, frissítve: 2015.01.01. https://software.intel.com/en-us/articles/3d-modeling-and-parallel-mesh-simplification, látogatva: 2017.10.28.
8. Erdős Zoltán: 3D-s animációt lejátszó és objektum-poligonszámot csökkentő alkalmazás forráskódja, https://github.com/ezszoftver/Zarovizsga, látogatva: 2017.10.28.
9. Valve Corporation honlapja, http://www.valvesoftware.com/, látogatva: 2017.10.28.
10. He Zhao: Progressive Meshes. 2008.04. http://hezhao.net/projects/progressive-meshes/, látogatva: 2017.10.28.
11. 3DRT: Goblin.smd, http://www.3DRT.com, látogatva: 2017.10.28.
12. Textúraillesztés egy háromszögre, https://www.slideshare.net/SyedZaidIrshad/opengl-texture-mapping, látogatva: 2017.11.12
13. Poligon (Triangle Fan), https://stackoverflow.com/questions/8043923/gl-triangle-fan-explanation, látogatva: 2017.11.12
14. Tér darabolása, http://slideplayer.com/slide/10896239/, látogatva: 2017.11.12
1. ábra: A MeshReducer program felülete [saját termék]
2. ábra: Sok vertexből álló poligon [saját ábra]
3. ábra: Textúraillesztés egy háromszögre
4. ábra: Térfelosztás poligon kereséséhez [saját ábra]
5. ábra: Poligoncsökkentés Blenderben (1/3. lépés): Kattintsunk a Modifies gombra. [saját kép]
6 ábra: Poligoncsökkentés Blenderben (1/3. lépés): Kattintsunk a Decimate gombra. [saját kép]
7. ábra: Poligoncsökkentés Blenderben (1/3. lépés): Csökkentés mértékének megadása. [saját kép]
8. ábra: Bal oldalon a 100%-os, jobb oldalon 75%-os poligonszámú modell [saját termék]
9. ábra: Legrövidebb él törlése [saját ábra]
10. ábra: A MeshReducer program felületének terve [saját termék]
12. ábra: A MeshReducer program objektumai közötti kapcsolat diagramja [saját ábra]
14. ábra: A MeshReducer program képernyője induláskor [saját termék]
15. ábra: A cottage.obj mejelenése a MeshReducer programban [saját termék]
16. ábra: A MeshReducer Options füle [saját termék]
17. ábra: A betöltött Antlion_guard_reference.smd a MeshReducer ablakban [saját termék]
18. ábra: Az idle.smd kiválasztása a MeshReducer felületén [saját termék]
19. ábra: Animáció az 50%-os részletezettségű Antlion guarddal [saját termék]
20. ábra: Ploligonszám csökkentett SMD fájl mentése [saját termék]
21. ábra: Poligonszám csökkentett OBJ fájl bentése [saját termék]
22. ábra: A MeshReducer About ablaka [saját termék]
|
Saját készítésű ingyenes játékaimat és azok forráskódját saját weboldalamon, a http://ezszoftver.atw.hu/-n osztom meg. |
|
|
A http://ezszoftver.atw.hu/ weboldal játékainak forráskódjai és a legfrissebb, még be nem felyezett fejlesztéseim a http://github.com/ezszoftver-en érhetők el. |
|
|
A Facebookon a http://facebook.com/ezszoftver lapon tájékoztatom az érdeklődőket a weboldal legfrissebb újdonságairól. |
|